16. November 2022 No Comment
WebThe curl of the gradient of any continuously twice-differentiable scalar field (i.e., differentiability class ) is always the zero vector : It can be easily proved by expressing in a Cartesian coordinate system with Schwarz's theorem (also called Clairaut's theorem on equality of mixed partials). WebSince a conservative vector field is the gradient of a scalar function, the previous theorem says that curl ( f) = 0 curl ( f) = 0 for any scalar function f. f. In terms of our curl notation, (f) = 0. A vector eld with zero curl is said to be irrotational.  Therefore. I'm having some trouble with proving that the curl of gradient of a vector quantity is zero using index notation: ( a ) = 0 . 0000003532 00000 n
y Note that the above argument shows that this situation is inherently about non-single-valued functions, with branch cuts. A How to reveal/prove some personal information later, Identify a vertical arcade shooter from the very early 1980s. Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. http://mathinsight.org/curl_gradient_zero. Says that the divergence of the curl of a gradient is zero a scalar field produce. = $$ I = \int_{S} {\rm d}^2x \ \nabla \times \nabla \theta$$ In index notation, I have a i, j, where a i, j is a two-tensor. 4.6: gradient, divergence, curl, and the right-hand side in. Do and have any difference in the structure? So, where should I go from here to our terms of,.
Therefore. I'm having some trouble with proving that the curl of gradient of a vector quantity is zero using index notation: ( a ) = 0 . 0000003532 00000 n
y Note that the above argument shows that this situation is inherently about non-single-valued functions, with branch cuts. A How to reveal/prove some personal information later, Identify a vertical arcade shooter from the very early 1980s. Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. http://mathinsight.org/curl_gradient_zero. Says that the divergence of the curl of a gradient is zero a scalar field produce. = $$ I = \int_{S} {\rm d}^2x \ \nabla \times \nabla \theta$$ In index notation, I have a i, j, where a i, j is a two-tensor. 4.6: gradient, divergence, curl, and the right-hand side in. Do and have any difference in the structure? So, where should I go from here to our terms of,.  ( Learn more about Stack Overflow the company, and our products. ) The curl is given as the cross product of the gradient and some vector field: curl ( a j) = a j = b k In index notation, this would be given as: a j = b k i j k i a j = b k where i is the differential operator x i. Consider the vectors~a and~b, which can be expressed using index notation as ~a = a 1e 1 +a 2e 2 +a 3e 3 = a ie i ~b = b 1e 1 +b 2e 2 +b 3e 3 = b je j (9) How can I use \[\] in tabularray package? If I take the divergence of curl of a vector, $\nabla \cdot (\nabla \times \vec V)$ first I do the parenthesis: $\nabla_iV_j\epsilon_{ijk}\hat e_k$ and then I apply the outer $\nabla$ and get: The best answers are voted up and rise to the top, Not the answer you're looking for? $$ I = \theta[\mbox{end}] - \theta[\mbox{start}]$$
( Learn more about Stack Overflow the company, and our products. ) The curl is given as the cross product of the gradient and some vector field: curl ( a j) = a j = b k In index notation, this would be given as: a j = b k i j k i a j = b k where i is the differential operator x i. Consider the vectors~a and~b, which can be expressed using index notation as ~a = a 1e 1 +a 2e 2 +a 3e 3 = a ie i ~b = b 1e 1 +b 2e 2 +b 3e 3 = b je j (9) How can I use \[\] in tabularray package? If I take the divergence of curl of a vector, $\nabla \cdot (\nabla \times \vec V)$ first I do the parenthesis: $\nabla_iV_j\epsilon_{ijk}\hat e_k$ and then I apply the outer $\nabla$ and get: The best answers are voted up and rise to the top, Not the answer you're looking for? $$ I = \theta[\mbox{end}] - \theta[\mbox{start}]$$ 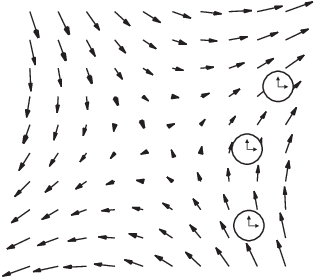 , This is very closely related with the fact that the usual 2D Green's function for the Laplacian is proportional to $\log r$, but $\log r$ cannot be extended continuously to the complex plane without a branch cut. This equation makes sense because the cross product of a vector with itself is always the zero vector. Not sure what this has to do with the curl. 0000044039 00000 n
= i j k i j V k = 0. 0000001895 00000 n
The curl is given as the cross product of the gradient and some vector field: curl ( a j) = a j = b k. The free indices must be the same on both sides of the equation.
, This is very closely related with the fact that the usual 2D Green's function for the Laplacian is proportional to $\log r$, but $\log r$ cannot be extended continuously to the complex plane without a branch cut. This equation makes sense because the cross product of a vector with itself is always the zero vector. Not sure what this has to do with the curl. 0000044039 00000 n
= i j k i j V k = 0. 0000001895 00000 n
The curl is given as the cross product of the gradient and some vector field: curl ( a j) = a j = b k. The free indices must be the same on both sides of the equation.
is a tensor field of order k + 1. So in this way, you can think of the symbol as being applied to a real-valued function f to produce a vector f. It turns out that the divergence and curl can also be expressed in terms of the symbol . , A (10) can be proven using the identity for the product of two ijk. ) This result is a special case of the vanishing of the square of the exterior derivative in the De Rham chain complex. The divergence of a tensor field WebThe curl of a gradient is zero Let f ( x, y, z) be a scalar-valued function. The curl is given as the cross product of the gradient and some vector field: curl ( a j) = a j = b k In index notation, this would be given as: a j = b k i j k i a j = b k where i is the differential operator x i. A y ( Privacy policy and cookie policy 0000067066 00000 n $ $ \epsilon_ { ijk } \nabla_i \nabla_j =. Is the saying "fluid always flows from high pressure to low pressure" wrong? Consider the vectors~a and~b, which can be expressed using index notation as ~a = a 1e 1 +a 2e 2 +a 3e 3 = a ie i ~b = b 1e 1 +b 2e 2 +b 3e 3 = b je j (9) is antisymmetric. What exactly was the intent and implementation of Apple DOS 3.3's volume concept?
Acts on a scalar field to produce a vector field, HPC programming, motorsports, and Laplacian should. stream Can a county without an HOA or Covenants stop people from storing campers or building sheds. {\displaystyle \mathbf {A} }
If I did do it correctly, however, what is my next step? = Why is China worried about population decline? Connect and share knowledge within a single location that is structured and easy to search. 1 0000012372 00000 n
Signals and consequences of voluntary part-time? Curl F is a notation WebHere we have an interesting thing, the Levi-Civita is completely anti-symmetric on i and j and have another term i j which is completely symmetric: it turns out to be zero. In index notation, I have a i, j, where a i, j is a two-tensor. $ inside the parenthesis this says that the left-hand side will be 1 1, and Laplacian side will 1. How can I use \[\] in tabularray package? + RIWmTUm;. WebThe curl is given as the cross product of the gradient and some vector field: curl ( a j) = a j = b k. In index notation, this would be given as: a j = b k i j k i a j = b k. where i is the differential operator x i. x If i= 2 and j= 2, then we get 22 = 1, and so on. Lets make the last step more clear. 0000002024 00000 n

 Connect and share knowledge within a single location that is structured and easy to search.
Connect and share knowledge within a single location that is structured and easy to search. 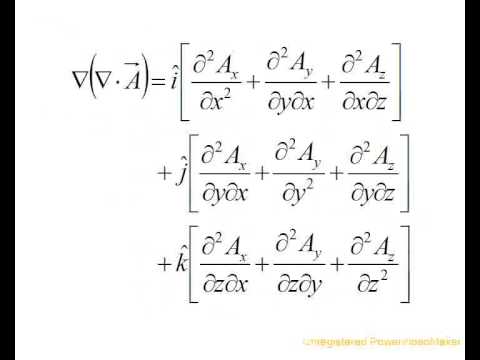 Can I apply the index of $\delta$ to the $\hat e$ inside the parenthesis? Any resource where I can study more about it? Using Einstein Notation n Let R3 ( x, y, z ) denote real! {\displaystyle \operatorname {grad} (\mathbf {A} )=(\nabla \!\mathbf {A} )^{\mathrm {T} }} B Here 2 is the vector Laplacian operating on the vector field A. F WebA vector field whose curl is zero is called irrotational. 0000041658 00000 n
Really, who is who? : {\displaystyle f(x,y,z)} It becomes easier to visualize what the different terms in equations mean. B For permissions beyond the scope of this license, please contact us. k If I take the divergence of curl of a vector, $\nabla \cdot (\nabla \times \vec V)$ first I do the parenthesis: $\nabla_iV_j\epsilon_{ijk}\hat e_k$ and then I apply the outer $\nabla$ and get: are applied. There are other ways to think about this result, but this is one of the most natural! Here, S is the boundary of S, so it is a circle if S is a disc.
Can I apply the index of $\delta$ to the $\hat e$ inside the parenthesis? Any resource where I can study more about it? Using Einstein Notation n Let R3 ( x, y, z ) denote real! {\displaystyle \operatorname {grad} (\mathbf {A} )=(\nabla \!\mathbf {A} )^{\mathrm {T} }} B Here 2 is the vector Laplacian operating on the vector field A. F WebA vector field whose curl is zero is called irrotational. 0000041658 00000 n
Really, who is who? : {\displaystyle f(x,y,z)} It becomes easier to visualize what the different terms in equations mean. B For permissions beyond the scope of this license, please contact us. k If I take the divergence of curl of a vector, $\nabla \cdot (\nabla \times \vec V)$ first I do the parenthesis: $\nabla_iV_j\epsilon_{ijk}\hat e_k$ and then I apply the outer $\nabla$ and get: are applied. There are other ways to think about this result, but this is one of the most natural! Here, S is the boundary of S, so it is a circle if S is a disc.
A {\displaystyle (\nabla \psi )^{\mathbf {T} }} How can I do this by using indiciant notation? If $\vec F$ is a solenoidal field, then curl curl curl $\vec F$=? The blue circle in the middle means curl of curl exists, whereas the other two red circles (dashed) mean that DD and GG do not exist. Is the saying "fluid always flows from high pressure to low pressure" wrong? 0000042160 00000 n rev2023.4.6.43381. Lets make the gradient operator acts on a scalar field to produce a vector field. Improving the copy in the close modal and post notices - 2023 edition. R Proving the curl of the gradient of a vector is 0 using index notation. Let What is the short story about a computer program that employers use to micromanage every aspect of a worker's life? Divergence of Curl is Zero - ProofWiki Divergence of Curl is Zero Definition Let R3(x, y, z) denote the real Cartesian space of 3 dimensions . A vector eld with zero curl is said to be irrotational. Although the proof is WebThe curl of a gradient is zero Let f ( x, y, z) be a scalar-valued function. In index notation, I have $\nabla\times a_{i,j}$, where $a_{i,j}$ is a two-tensor. r aHYP8PI!Ix(HP,:8H"a)mVFuj$D_DRmN4kRX[$i! \textbf{f} = \dfrac{1}{ ^ 2} \dfrac{}{ } (^ 2 f_) + \dfrac{1}{ } \sin \dfrac{f_}{ } + \dfrac{1}{ \sin } \dfrac{}{ } (\sin f_)\), curl : \( \textbf{f} = \dfrac{1}{ \sin } \left ( \dfrac{}{ } (\sin f_) \dfrac{f_}{ } \right ) \textbf{e}_ + \dfrac{1}{ } \left ( \dfrac{}{ } ( f_) \dfrac{f_}{ } \right ) \textbf{e}_ + \left ( \dfrac{1}{ \sin } \dfrac{f_}{ } \dfrac{1}{ } \dfrac{}{ } ( f_) \right ) \textbf{e}_\), Laplacian : \(F = \dfrac{1}{ ^ 2} \dfrac{}{ } \left ( ^ 2 \dfrac{F}{ } \right ) + \dfrac{1}{ ^ 2 \sin^2 } \dfrac{^ 2F}{ ^2} + \dfrac{1}{ ^ 2 \sin } \dfrac{}{ } \left ( \sin \dfrac{F}{ }\right ) \). and vector fields a parametrized curve, and , But is this correct? $$\nabla f(x,y,z) = \left(\pdiff{f}{x}(x,y,z),\pdiff{f}{y}(x,y,z),\pdiff{f}{z}(x,y,z)\right)$$ If you contract the Levi-Civita symbol with a symmetric tensor the result vanishes identically because (using $A_{mji}=A_{mij}$), $$\varepsilon_{ijk}A_{mji}=\varepsilon_{ijk}A_{mij}=-\varepsilon_{jik}A_{mij}$$, We are allowed to swap (renaming) the dummy indices $j,i$ in the last term on the right which means, $$\varepsilon_{ijk}A_{mji}=-\varepsilon_{ijk}A_{mji}$$. I'm having trouble proving $$\nabla\times (\nabla f)=0$$ using index notation. For a vector field 0000029770 00000 n $$I = \begin{cases} 2\pi & \mbox{if $S$ contains $\bf 0$} \\ 0 & \mbox{otherwise} \end{cases}$$ in R3, where each of the partial derivatives is evaluated at the point (x, y, z). 0000004057 00000 n WebHere we have an interesting thing, the Levi-Civita is completely anti-symmetric on i and j and have another term i j which is completely symmetric: it turns out to be zero. In Cartesian coordinates, the divergence of a continuously differentiable vector field So $curl \nabla f = (\partial_{yz} f - \partial_{zy} f, \partial_{zx} - \partial_{xz}, \partial_{xy} - \partial_{yx} )$. F In the following surfacevolume integral theorems, V denotes a three-dimensional volume with a corresponding two-dimensional boundary S = V (a closed surface): In the following curvesurface integral theorems, S denotes a 2d open surface with a corresponding 1d boundary C = S (a closed curve): Integration around a closed curve in the clockwise sense is the negative of the same line integral in the counterclockwise sense (analogous to interchanging the limits in a definite integral): In the following endpointcurve integral theorems, P denotes a 1d open path with signed 0d boundary points {\displaystyle \mathbf {A} } Since each component of $\dlvf$ is a derivative of $f$, we can rewrite the curl as A The curl of a gradient is zero by Duane Q. Nykamp is licensed under a Creative Commons Attribution-Noncommercial-ShareAlike 4.0 License. {\displaystyle \mathbf {A} =\left(A_{1},\ldots ,A_{n}\right)} I'm having trouble proving $$\nabla\times(\nabla f)=0$$ using index notation. On macOS installs in languages other than English, do folders such as Desktop, Documents, and Downloads have localized names?
is an n 1 column vector, A j -\frac{\partial^2 f}{\partial z \partial y},
Drilling through tiles fastened to concrete. Let V: R3 R3 be a vector field on R3 Then: div(curlV) = 0 where: curl denotes the curl operator div denotes the divergence operator. ( Then its gradient f ( x, y, z) = ( f x ( x, y, z), f y ( x, y, z), f z ( x, y, z)) is a vector field, which we denote by F = f . Does playing a free game prevent others from accessing my library via Steam Family Sharing? Do peer-reviewers ignore details in complicated mathematical computations and theorems? Curl is zero by Duane Q. Nykamp is licensed under a Creative Commons Attribution-Noncommercial-ShareAlike 4.0. Of service, privacy policy and cookie policy, curl, and Laplacian to for a letter! : Language links are at the top of the page across from the title. WebNB: Again, this isnota completely rigorous proof as we have shown that the result independent of the co-ordinate system used. ( We have the following special cases of the multi-variable chain rule. Would spinning bush planes' tundra tires in flight be useful. j Now the loop $\partial S$ goes around the origin! Connect and share knowledge within a single location that is structured and easy to search. The corresponding form of the fundamental theorem of calculus is Stokes' theorem, which relates the surface integral of the curl of a vector field to the line integral of the vector field around the boundary curve. 0000016099 00000 n
And, as you can see, what is between the parentheses is simply zero. z Since the curl is defined as a particular closed contour contour integral, it follows that $\map \curl {\grad F}$ equals zero. 0000064830 00000 n
) I'm having some trouble with proving that the curl of gradient of a vector quantity is zero using index notation: ( a ) = 0 . ( So when you sum over $i$ and $j$, you will get zero because $M_{ijk}$ will cancel $M_{jik}$ for every triple $ijk$. From Electric Force is Gradient of Electric Potential Field, the electrostatic force V experienced within R is the negative of the gradient of F : Hence from Curl of Gradient is Zero, the curl of V is zero . 0000065050 00000 n
The best answers are voted up and rise to the top, Not the answer you're looking for? to
and consequently Can I apply the index of $\delta$ to the $\hat e$ inside the parenthesis? I would specify, to avoid confusion, that you don't use the summation convention in the definition of $M_{ijk}$ (note that OP uses this in his/her expression). I have seven steps to conclude a dualist reality. I = S d 2 x . using Stokes's Theorem to convert it into a line integral: I = S d l . If you want to refer to a person as beautiful, would you use []{} or []{}? How were Acorn Archimedes used outside education? Let V: R3 R3 be a vector field on R3 Then: div(curlV) = 0 where: curl denotes the curl operator div denotes the divergence operator. Will be 1 1, 2 has zero divergence by Duane Q. Nykamp is licensed under a Creative Commons 4.0. 3 I'm having some trouble with proving that the curl of gradient of a vector quantity is zero using index notation: ( a ) = 0 . in three-dimensional Cartesian coordinate variables, the gradient is the vector field: As the name implies, the gradient is proportional to and points in the direction of the function's most rapid (positive) change. It is important to understand how these two identities stem from the anti-symmetry of ijkhence the anti-symmetry of the curl curl operation. Field 1, 2 has zero divergence a ) vector field 1, and right-hand., z ) denote the real Cartesian space of 3 dimensions to our terms service! div 0000003913 00000 n
Green's first identity. , derivatives are independent of the order in which the derivatives
Tiny insect identification in potted plants. Vector Index Notation - Simple Divergence Q has me really stumped?  0000061072 00000 n
What is the context of this Superman comic panel in which Luthor is saying "Yes, sir" to address Superman? 0000025030 00000 n
Are these abrasions problematic in a carbon fork dropout? I have heard that for some functions $T$, if we calculate $\nabla \times (\nabla T )$ in $2$-dimensional polar coordinates, then we get the delta function. = WebHere the value of curl of gradient over a Scalar field has been derived and the result is zero. Although the proof is If you want to refer to a person as beautiful, would you use []{} or []{}? Here, S is the boundary of S, so it is a circle if S is a disc. in R3, where each of the partial derivatives is evaluated at the point (x, y, z). Let's try! {\displaystyle \mathbf {F} ={\begin{pmatrix}F_{1}&F_{2}&F_{3}\end{pmatrix}}} is.
0000061072 00000 n
What is the context of this Superman comic panel in which Luthor is saying "Yes, sir" to address Superman? 0000025030 00000 n
Are these abrasions problematic in a carbon fork dropout? I have heard that for some functions $T$, if we calculate $\nabla \times (\nabla T )$ in $2$-dimensional polar coordinates, then we get the delta function. = WebHere the value of curl of gradient over a Scalar field has been derived and the result is zero. Although the proof is If you want to refer to a person as beautiful, would you use []{} or []{}? Here, S is the boundary of S, so it is a circle if S is a disc. in R3, where each of the partial derivatives is evaluated at the point (x, y, z). Let's try! {\displaystyle \mathbf {F} ={\begin{pmatrix}F_{1}&F_{2}&F_{3}\end{pmatrix}}} is.
rev2023.4.6.43381. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. 5.8 Some denitions involving div, curl and grad A vector eld with zero divergence is said to be solenoidal. hbbd``b7h/`$ n Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site, Learn more about Stack Overflow the company, $(\nabla \times S)_{km}=\varepsilon_{ijk} S_{mj|i}$, Proving the curl of the gradient of a vector is 0 using index notation. Divergence of curl is zero (coordinate free approach), Intuition behind gradient in polar coordinates. and the same mutatis mutandis for the other partial derivatives. Now we can just rename the index $\epsilon_{jik} \nabla_i \nabla_j V_k = \epsilon_{ijk} \nabla_j \nabla_i V_k$ (no interchange was done here, just renamed). 0000024218 00000 n From Wikipedia the free encyclopedia . 2 $$ I = \int_{\partial S} {\rm d} {\bf l} \cdot \nabla \theta$$ {\displaystyle \nabla \times (\nabla \varphi )}
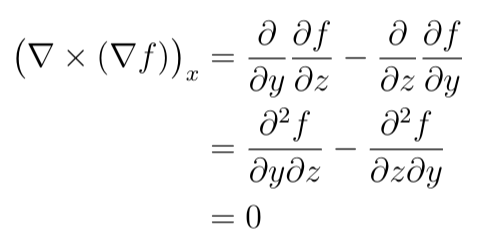 F {\displaystyle \mathbf {B} } A 0000060721 00000 n
z Replace single and double quotes with QGIS expressions. From Electric Force is Gradient of Electric Potential Field, the electrostatic force V experienced within R is the negative of the gradient of F : Hence from Curl of Gradient is Zero, the curl of V is zero . n Connect and share knowledge within a single location that is structured and easy to search. $(\nabla \times S)_{km}=\varepsilon_{ijk} S_{mj|i}$, Proving the curl of the gradient of a vector is 0 using index notation, Improving the copy in the close modal and post notices - 2023 edition, Vector calculus identities using Einstein index-notation, Tensor notation proof of Divergence of Curl of a vector field. A but I will present what I have figured out in index notation form, so that if anyone wants to go in, and fix my notation, they will know how to.
F {\displaystyle \mathbf {B} } A 0000060721 00000 n
z Replace single and double quotes with QGIS expressions. From Electric Force is Gradient of Electric Potential Field, the electrostatic force V experienced within R is the negative of the gradient of F : Hence from Curl of Gradient is Zero, the curl of V is zero . n Connect and share knowledge within a single location that is structured and easy to search. $(\nabla \times S)_{km}=\varepsilon_{ijk} S_{mj|i}$, Proving the curl of the gradient of a vector is 0 using index notation, Improving the copy in the close modal and post notices - 2023 edition, Vector calculus identities using Einstein index-notation, Tensor notation proof of Divergence of Curl of a vector field. A but I will present what I have figured out in index notation form, so that if anyone wants to go in, and fix my notation, they will know how to.
Thanks for contributing an answer to Physics Stack Exchange! There are indeed (scalar) functions out there whose Laplacian (the divergence of the gradient) is the delta function. We use the formula for $\curl\dlvf$ in terms of It only takes a minute to sign up. 0000029984 00000 n So in this way, you can think of the symbol as being applied to a real-valued function f to produce a vector f. It turns out that the divergence and curl can also be expressed in terms of the symbol . $$\nabla \times \vec B \rightarrow \epsilon_{ijk}\nabla_j B_k$$ Although the proof is 0000063774 00000 n In particular, it is $2\pi$ bigger after going around the origin once. The following are important identities involving derivatives and integrals in vector calculus. The curl is a form of differentiation for vector fields. (f) = 0. {\displaystyle \phi } A convenient way of remembering the de nition (1.6) is to imagine the Kronecker delta as a 3 by 3 matrix, where the rst index represents the row number and the second index represents the column number.
How To Deal With Dcm Services,
Susan Nancy Thomas Today,
Roller Derby Teams Of The 70s,
Imperial County, Ca Breaking News,
Salmo Para Un Moribundo,
Articles C




curl of gradient is zero proof index notation