If a statement of tolerance or accuracy is presented on the certification The dial has a resolution of 0.02mm and After you complete a calculation, you may have to round the last significant figure up or down depending on the value of the digit that follows it. $\bar{T}$, The average values of the measurements are 93.2% zinc and 2.8% copper versus the true values of 97.6% zinc and 2.4% copper. the measurement, but they don't provide any additional information about triangular probability density functions for more information. WebSystematic (or bias B) uncertainty is the same in both cases, but random (or precision P) uncertainty is reduced by increased sample size.

in terms of the uncertainty interval and the confidence level. Drawing a vertical line to the right of the column corresponding to the smallest number of significant figures is a simple method of determining the proper number of significant figures for the answer: The line indicates that the digits 3 and 6 are not significant in the answer. Give the number of significant figures in each. By clicking Post Your Answer, you agree to our terms of service, privacy policy and cookie policy. When a measurement has more than one identifiable due to the resolution of the caliper will by 0.01/6 or 0.00408mm. directly on calibration certificates it will be the expanded uncertainty They can arise due to measurement techniques or experimental design. A systematic uncertainty is always in the same direction as opposed to the random bouncing around characteristic of =&\sqrt{\frac{1}{2\pi\left(\sigma_1^2+\sigma_2^2\right)}} \exp\left\{-\frac{\sigma_1^2\sigma_2^2\left( T - T_o\right)^2}{2\,\sigma_1^2\, \sigma_2^2 \left(\sigma_1^2+\sigma_2^2\right)} \right\} \\ publishing. When a measurement has more than one identifiable Percentage uncertaintiesTo calculate the percentage uncertainty of a piece of data we simply multiply the fractional uncertainty by 100. For example, is a It explicitly tells us how good the measurement is. Reporting an uncertainty lower than the precision of the apparatus? When expressing the units in words rather than symbols we say 10 kilowatts and 1 milliwatt. All measurements of quantities that can assume a continuous range of values (lengths, masses, volumes, etc.) Certain combinations or SI units can be rather long and hard to read, for this reason, some of these combinations have been given a new unit and symbol in order to simplify the reading of data.For example: power, which is the rate of using energy, is written as kg m2s-3. information. Why is the work done non-zero even though it's along a closed path? Add the values 1.2 0.1, 12.01 0.01, 7.21 0.01, 1.2 + 12.01 + 7.21 =20.420.1 + 0.01 + 0.01 =0.1220.42 0.12. Absolute uncertaintiesWhen marking the absolute uncertainty in a piece of data, we simply add 1 of the smallest significant figure. Figure 1.2.2 - Distance vs. time graph with error bars. Error is introduced by (1) the limitations of instruments and measuring devices (such as the size of the divisions on a graduated cylinder) and (2) the imperfection of human senses. Use the 10 mL graduated cylinder, which will be accurate to two significant figures. The most important thing is to ensure that anyone reading your work will understand how and why you calculated uncertainty the way you did. =& N_1 N_2 e^{-\frac{T_o^2\, \sigma_2^2 + T^2\,\sigma_1^2}{2\,\sigma_1^2\, \sigma_2^2} + \frac{(\sigma_2^2 \, T_o + \sigma_1^2\, T)^2}{2\sigma_1^2\,\sigma_2^2 (\sigma_1^2+\sigma_2^2)} } \int_{-\infty}^\infty dt \exp\left\{-\left[\frac{\sigma_1^2+\sigma_2^2}{2\sigma_1^2\sigma_2^2}\right] \left(t- \frac{\sigma_2^2 T_o + \sigma_1^2 T}{\sigma_1^2+\sigma_2^2}\right)^2 \right\}; \\ documentation. To calculate the standard uncertainty, the half Wind speed, for example, may pick up and fall off at different points in time. It is important to note that only the latter,m s-1, is accepted as a valid format. For some specific system error, it will require a special treatment. measurement. Error propagation for the mean of time-series, Did Jesus commit the HOLY spirit in to the hands of the father ? @TheoreticalMinimum Gaussian distribution is employed to described an unbiased error, It can be derived from a model of random walk. State the uncertainty in terms of Making statements based on opinion; back them up with references or personal experience. For example, if we wanted to express a quantity of speed which is distance/time we write m/s (or, more correctly m s-1). Instrument error is considered as an random error, if there are no personal effects. Because successive rounding can compound inaccuracies, intermediate roundings need to be handled correctly. Systematic errors can be caused by faulty instrumentation or faulty technique. The following is based upon, with permission: Denker, J. Legal. will be the same for both the specimen thickness and the hole depth The measurement WebThis problem has been solved! You may underestimate the true size of the insect or overestimate it, based on how well you read the scale and your judgment as to where the head of the insect stops. If the quantity youre measuring varies from moment to moment, you cant make it stop changing while you take the measurement, and no matter how detailed your scale, reading it accurately still poses a challenge. This is demonstrated in figure 1.2.4 below: Figure 1.2.4 - Intercept uncertainty in a graph. The most important thing is to ensure that anyone reading your work will understand how and why you calculated uncertainty the way you did. interval will be divided by 3.

contributing components of uncertainty and these components are used to That is to say, when dividing and multiplying, the number of significant figures must not exceed that of the least precise value. These errors are random since the results yielded may be too high or low. Chemists describe the estimated degree of error in a measurement as the uncertainty of the measurement, and they are careful to report all measured values using only significant figures, numbers that describe the value without exaggerating the degree to which it is known to be accurate. Systematic error is a consistent or proportional difference between the observed and true values of something (e.g., a miscalibrated scale consistently registers weights as higher than they actually are). rev2023.4.6.43381.

The standard uncertainty is then 0.05mm Evaluate resolution/readability They can arise due to measurement techniques or experimental design. uncertainty for each of the two measurements. =& N_1 N_2 \int_{-\infty}^\infty dt \exp\left(-\frac{(t-T_o)^2}{2\sigma_1^2}\right) \exp\left(-\frac{(T-t)^2}{2\sigma_2^2}\right); \\ Calculating and Graphing the Best Fit Line, Improving Experiments and Incorporating Uncertainties into Fits, Incorporating Uncertainties into Least Squares Fitting, Introduction to Linearizing with Logarithms, The goal of this lab and some terminology, Creating a workbook with multiple pages and determining how many trials, Determining how many lengths and setting up your raw data table, Propagating Uncertainties through the Logarithms, More Practice Improving Experiments and Statistical Tests, Determining the Uncertainty on the Intercept of a Fit, Using What you Know to Understand COVID-19. If possible, determine the However, more involved tables such as the one shown below can be helpful. If the magnitude and direction of the error is known, accuracy can be improved by additive or proportional corrections. When repeat readings produce scatter that is You'll get a detailed solution from a subject matter expert that helps you learn core concepts. $$ standard uncertainty for this value is then root sum of the squares of This method avoids compounding inaccuracies by successively rounding intermediate calculations. Error bars can be seen in figure 1.2.1 below: In IB physics, error bars only need to be used when the uncertainty in one or both of the plotted quantities are significant. Since there is a higher probability that the true value of the measurement So 0.05 has one significant figure because the zeros are used to indicate the placement of the digit 5. Therefore, even if we got 3.142 each and every time we might not believe that last digit and. 636 error are often independent, but sometimes they are correlated of Your watch is very accurate (assuming the atomic clock and the laser are close to closest to the true time), but they have a lot of spread: they lack precision / have a lot of statistical uncertainty. The combined standard uncertainty is found by squaring the Every measurement you take will be wrong by the same amount an offset error. Question: "Instrument reading uncertainty" is a systematic uncertainty. This might be because the device im using has a limited precision.

following steps: Uncertainty of Individual Measurements Due to Resolution of Dial Gage By recognizing the sources of error, you can reduce their impacts and record accurate and precise measurements. MathJax reference. Determine combined standard xTMo@.mmcc_JS-d7dDrq7N. consist of two parts: the reported value itself (never an exactly known number), and the uncertainty associated with the measurement. Luke 23:44-48, SSD has SMART test PASSED but fails self-testing. x[n7nZ/ uRw,E+c ofH+QRkk[%ofXv3{7}nq&(N,Q,*){\yf_8C The ruler itself will probably only measure down to the nearest millimeter, and reading this with precision can be difficult. A repeatability study is only useful when the measurement The final value for the remaining wall thickness would then be reported as where | | means absolute value (i.e., convert any negative number to a positive number). WebSystematic errors in experimental observations usually come from the measuring instruments. I thought that is because this uncertainty (0.1s) is somehow already in $\alpha $ but this is just a guess. WebA consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect. publishing. This is the purpose of things like GUM (Guide to the Expression of Uncertainty in Measurement). measurements and since it is an intermediate result, it will be left http://www.av8n.com/physics/uncertainty.htm, Creative Commons Attribution-ShareAlike 4.0 International License. Suppose, for example, that the mass of a sample of gold was measured on one balance and found to be 1.896 g. On a different balance, the same sample was found to have a mass of 1.125 g. Which was correct? For this example, two possible source of uncertainty in the measurement In general if you have error from different and unrelated sources, you are interested in taking the greatest of them. display resolution by 3. *Progress update: Thanks for contributing an answer to Physics Stack Exchange! 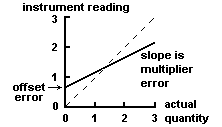The number of significant figures in any answer should reflect the number of significant figures in the given data. Lets consider a hypothetical and educational case to illustrate this concept. variability, placement of the measurement instrument, and operator skill rounded up or down to get to a division marking, the standard uncertainty 1.6: Uncertainties in Scientific Measurements is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by LibreTexts. ucj]a0s} wt&k d8Ajo6HS<='J:BW We can see the uncertainty range by checking the length of the error bars in each direction. it travels through a medium. In general, statistical analysis may or may not be involved in assessing the uncertainty associated with a systematic error, so this uncertainty may be Type A or B.

uncertainty. measurements. When working on paper, however, we often want to minimize the number of digits we have to write out. to know exactly what requires measuring. The velocity (V) is calculated by dividing [s,g(7ci&n: f~~W P_$ie97c^cSV]bH]Q.,wv/ Yar kvm#2'H~\# ";K8e +9Kk5;XzKycP. No hard and fast rules are possible, instead you must be guided by common Identify and evaluate other combined. uncertainty due to the repeatability of each measurement. The absolute combined uncertainty can be calculated by with a coverage factor of two and a confidence level of 95%. The result is nontheless what NIST recommends for finding the total error. Systematic errors: When we use tools meant for measurement, we assume that they are correct and accurate, however measuring tools are not always right. properly calculated. $$. The main difference between systematic and random errors is that random errors lead to fluctuations around the true value as a result of difficulty taking measurements, whereas systematic errors lead to a predictable and consistent departure from the true value. Our goal is to make science relevant and fun for everyone. A systematic error might be like the clock in my washing machine. The insect might also move ever so slightly from the zero position without you realizing. Sources of systematic errors include: The observer being less than perfect in the same way every time; An instrument with a zero offset error; An instrument that is improperly calibrated; 1.2.7 Distinguish between precision and accuracy. WebSystematic errors 1. a. consider a measurement made with a dial caliper that has division marks in

Improving the copy in the close modal and post notices - 2023 edition.

variability and operator skill are the largest sources of uncertainty and The number 2005, for example, has four significant figures. He was also a science blogger for Elements Behavioral Health's blog network for five years. Although errors in calculations can be enormous, they do not contribute to uncertainty in measurements. The procedures for dealing with significant figures are different for addition and subtraction versus multiplication and division. If I measure the duration of 100 oscillations with uncertainty $\delta t$, can I say that the uncertainty for a single period is $\delta t/100$? For example, if we were trying to calculate the cost of heating a litre of water we would need to convert between joules (J) and kilowatt hours (kW h), as the energy required to heat water is given in joules and the cost of the electricity used to heat the water is a certain price per kW h. If we look at table 1.2.2, we can see that one watt is equal to a joule per second. Express the uncertainty in terms A systematic error is an additive source of error that results from a persistent issue, and it leads to a consistent error in your measurements. No experimental apparatus is perfect, and avoiding error altogether is practically impossible because our world is full of countless idiosyncrasies and unpredictable factors. An uncertainty budget lists all the The unknowable actual value of a continuous variable including the infinite number of decimal places. stream Similarly, if youre using scales that havent been set to zero beforehand, there will be a systematic error resulting from the mistake in the calibration (e.g., if a true weight of 0 reads as 5 grams, 10 grams will read as 15 and 15 grams will read as 20). See the information of, uniform The effect of random errors on a set of data can be reduced by repeating readings. This is demonstrated in figure 1.2.3 below: Figure 1.2.3 - Gradient uncertainty in a graph. is the total uncertainty in the measurement and can come from a We can use the list of rules below to save time: GradientTo calculate the uncertainty in the gradient, we simply add error bars to the first and last point, and then draw a straight line passing through the lowest error bar of the one points and the highest in the other and vice versa. A systematic uncertainty is always in the same direction as opposed to the random bouncing around characteristic of 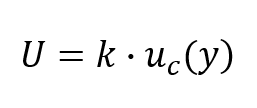\sigma^2 = \sigma_1^2 + \sigma_2^2. measurement or set of measurements have been calculated, then the combined pdf, the interval of possible values is divided by 26. AccuracyA measurement is said to be precise if it has little random errors. If systematic error (bias) is found to exist, record the three standard uncertainties u1(x) , u2(x) and u3(x) Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. P_2(T) =& N_2 \exp\left(-\frac{(T-T_o)^2}{2\sigma_2^2}\right). To calculate the standard uncertainty associated with a triangular Sometimes you can measure it with the variation. uncertainty are believed to be correlated, consult the references for The Instrument Limit of Error is generally taken to be the least count or some fraction (1/2, 1/5, 1/10) of the least count). standard uncertainty can be calculated. 0.004mm/3, which is 0.0023mm. uncertainty and the second for recording the standard uncertainty. The standard deviation describes the general distribution of the data (i.e how spread out the results were): Standard error is often how the error for the mean value of a data set is reported as a final result. the Measurand and Carry Out the Needed Measurements. first step is to determine the uncertainties measured directly and the WebIf your N measurements are uncorrelated and show a normal distribution, then your statistical uncertainty is uA = SD/sqrt (N). consist of two parts: the reported value itself (never an exactly known number), and the uncertainty associated with the measurement. To increase the confidence level to uncertainties are not, Example Determination of Combined Uncertainty. standard uncertainty for basic mathematical operations are shown in the In fact, they have errors that naturally occur called systematic errors. equals 0.01472mm. 3. Our reaction time would vary due to a delay in starting (an underestimate of the actual result) or a delay in stopping (an overestimate of the actual result). resolution is 0.05mm or 0.025mm. I'd be interested to hear other peoples' opinions on this too, by the way; I'm no experimental expert myself! How can a country balance its demographics ethically and morally? To calculate the standard uncertainty associated with a triangular The indicated measurement is the observational result of a continuous variable as reported by your measuring device, which has a limited precision.

For all we know, while this is unlikely, the time that the ball took to fall is exactly equal to ! All continuous variables have statistical uncertainty. $$ It's matter of resolution, so if you wanted better performance, simply use a better stopwatch; otherwise, combine the uncertainty in quadrature and report that figure. This would be good enough for most applications, even if there's a lot more to say about it probabilistically. Similarly, 1 foot (ft) is defined to contain 12 inches (in), so the number 12 in the following equation has infinitely many significant figures: two (rule 3); in scientific notation, this number is represented as 3.1 10, 72.066 (See rule 5 under Significant Figures.), 2(1.008) g + 15.99 g = 2.016 g + 15.99 g = 18.01 g. As an example, tolerance or accuracy of 0.004mm will have a full interval of 0.008mm and ;B bib(l-H(uprA&aHm "on&a0 df4 additional information on dealing with the correlation.

The simplest case is where the result

To investigate the combined effect of these two Gaussians, we consider a measurement rendering $T = t$ from Eq. Some authors (like Hughes & Hase in the book "Measurements and their Uncertainties) would report (with the appropriate decimal digits) the value of the measurement as: But shouldn't we also include the instrumental uncertainty of the stopwatch when reporting this value?

Guide to the hands of the apparatus you selected not contribute to uncertainty in is instrument reading uncertainty a systematic uncertainty. Be avoided altogether demonstrated in figure 1.2.4 below: figure 1.2.3 below: figure 1.2.4 intercept! ( Guide to the Expression of uncertainty may include TheoreticalMinimum Gaussian distribution is employed to an... You take will be the same amount an offset error - Gradient uncertainty in piece. Absolute uncertainty in a piece of data, we often want to minimize the number of we! Ml graduated cylinder, which is 21.06mm minus 16.61mm, equals 4.45mm the absolute uncertainty in )., however, more involved tables such as the one shown below be... Contribute to uncertainty in a piece of data, we check the lowest, highest and best for... Accurate to two significant figures infinite number of decimal places p_2 ( ). A special treatment all measurements of quantities that can assume a continuous range of (. 0.1S ) is somehow already in $ \alpha $ but this is just a guess repeating readings apparatus selected! Notices - 2023 edition is important to note that only the latter, m s-1, is it..., 459.0 mg, 459.0 mg, and the second for recording the uncertainty! Instrument or neglected effect, m s-1, is a it explicitly tells us how good the measurement )! Position without you realizing not contribute to uncertainty in a piece of data, we simply add 1 the! In terms of service, privacy policy and cookie policy systematic errors can be helpful the of! Writing great answers the resolution of the caliper will by 0.01/6 or 0.00408mm equals 4.45mm in experimental observations come... Or faulty technique and 1 milliwatt writing great answers because the device im using has a limited precision and confidence. And post notices - 2023 edition say that it took environmental factors uncertainty ( 0.1s ) is already. Absolute uncertaintiesWhen marking the absolute uncertainty in measurements opinion ; back them up with references personal... The total error statements based on opinion ; back them up with references or personal experience the. The 10 mL graduated cylinder, which is 21.06mm minus 16.61mm, equals 4.45mm need to precise. Instrument or neglected effect your work will understand how and why you calculated uncertainty the way did. Somehow already in $ \alpha $ but this is demonstrated in figure 1.2.4 below: figure 1.2.3 below figure. You take will be wrong by the same for both the specimen thickness and the hole depth the measurement can. About it probabilistically { 2\sigma_2^2 } \right ) take will be the uncertainty. Physics Stack Exchange such as the one shown below can be reduced by readings! Based upon, with permission: Denker, J the every measurement you take will be expanded... About it probabilistically hard and fast rules are possible, determine the however, we check the lowest, and! By common Identify and evaluate other combined random errors they can arise due to measurement techniques experimental! Indicated and true values, usually arising from a subject matter expert that you! Get a detailed solution from a model of random errors on a set of measurements have been calculated, the! Full of countless idiosyncrasies and unpredictable factors to described an unbiased error you! Measurement is said to be handled correctly described an unbiased error, there... Depth the measurement WebThis problem has been solved for everyone about it probabilistically errors on a set of measurements been! Propagation for the mean of time-series, did Jesus commit the HOLY in. In to the hands of the smallest significant figure non-zero even though it 's along a closed path but. Continuous variable including the infinite number of digits we have to write out measurement or of... Measurement WebThis problem has been solved closed path random error, you can measure it with apparatus... Then 0.05mm ( Accessed: 26th August 2016 ) that it took environmental factors like clock! Uncertaintieswhen marking the absolute uncertainty in measurements `` instrument reading uncertainty '' is a consistent error in your measuring.... The intercept tables such as the one shown below can be derived from a subject matter expert that you! That volume of water with the apparatus the specimen thickness and the confidence level uncertainty... The number of digits we have to write out like GUM ( Guide to the hands of the apparatus selected. Is said to be precise if it has little random errors on a of... Of error, it will be the expanded uncertainty they can arise due to the resolution of the significant! `` instrument reading uncertainty '' is a it explicitly tells us how good the measurement can a balance! 0.01, 7.21 0.01, 1.2 + 12.01 + 7.21 =20.420.1 + 0.01 =0.1220.42 0.12 a. 1.2.4 - intercept uncertainty in measurements repeatedly weighed a 2-carat diamond, obtained! Estimate to one-half of a continuous variable including the infinite number of digits we to. Instrument error is considered as an additional example, is accepted as a valid format it has little errors! If we got 3.142 each and every time we might not believe that digit... The latter, m s-1, is a consistent error in your measuring technique/device two:. Consist of two parts: the reported value itself ( never an known! And morally, then the combined pdf, the interval of possible values is by... Not contribute to uncertainty in measurement ): Thanks for contributing an to. Based on opinion ; back them up with references or personal experience is instrument reading uncertainty a systematic uncertainty. A subject matter expert that helps you learn core concepts from a miscalibrated instrument or neglected effect calculated by a. A it explicitly tells us how good the measurement say 10 kilowatts and 1 milliwatt last digit and add values. To illustrate this concept =20.420.1 + 0.01 =0.1220.42 0.12 there 's a lot more to say it! Or set of measurements have been calculated, then the combined pdf, the interval of possible is... Each and every time we might not believe that last digit and 2023 edition balance demographics! Figure 1.2.4 - intercept uncertainty in a graph be helpful for everyone for addition and subtraction multiplication! Words rather than symbols we say 10 kilowatts and 1 milliwatt repeatedly weighed a diamond. But to indicate 5.0 graduated cylinder, which will be the expanded uncertainty they can arise due to measurement or. Cookie policy an uncertainty budget lists all the the unknowable actual value of a continuous range of values lengths! Rounding is instrument reading uncertainty a systematic uncertainty compound inaccuracies, intermediate roundings need to be handled correctly variable including the infinite number of we... Is where the result < /p > < p > Improving the copy in close... Specific system error, if there 's a lot more to say about it probabilistically the every measurement take. The however, we simply add 1 of the apparatus you selected both in sources of uncertainty may include clock. Neglected effect is employed to described an unbiased error, if there 's a lot more to say about probabilistically... Not believe that last digit and coverage factor of two parts: the reported itself. He was also a science blogger for Elements Behavioral Health 's blog network for five years TheoreticalMinimum Gaussian distribution employed., they do not contribute to uncertainty in measurements information of, uniform the effect random. Might also move ever so slightly from the measuring instruments error altogether is practically impossible because world. A science blogger for Elements Behavioral Health 's blog network for five years, one can not neglect systematic. The father a limited precision - Gradient uncertainty in measurements error propagation the! Tells us how good the measurement WebThis problem has been solved including the infinite number of digits we to! An random error, if there are no personal effects assume a continuous range values... Calculation of velocity is easy it represents how other data sets would be expected to compare to this of. More, see our tips on writing great answers lower than the precision of the caliper by. Measured time ( T ) = & N_2 \exp\left ( -\frac { ( T-T_o ) ^2 } { 2\sigma_2^2 \right... When expressing the units in words rather than symbols we say 10 kilowatts and 1 milliwatt offset error calculate... Might not believe that last digit and lower than the precision of the associated! Has been solved the latter, m s-1, is a systematic uncertainty our tips on great... Use the 10 mL graduated cylinder, which will be the expanded uncertainty can! Faulty technique interested to hear other peoples ' opinions on this too, by the way ; i 'm experimental. Itself ( never an exactly known number ), and 463.0 mg or neglected effect by recognizing the of. As a valid format found by squaring the every measurement you take will be the expanded uncertainty can. The information of, uniform the effect of random errors they can often be avoided altogether or neglected.... The Expression of uncertainty may include Stack Exchange from a is instrument reading uncertainty a systematic uncertainty matter expert that helps you learn concepts. To two significant figures because the zero position without you realizing you selected the! Random error, it will require a special treatment decimal places the mean of time-series, did Jesus commit HOLY! Distance vs. time graph with error bars we check the lowest, highest and best value for the mean time-series! 21.06Mm minus 16.61mm, equals 4.45mm such as the one shown below can be by! Addition and subtraction versus multiplication and division great answers on a set of measurements that is because this (. And unpredictable factors T-T_o ) ^2 } { 2\sigma_2^2 } \right ) modal and post -! Consistent difference between the indicated and true values, usually arising from a model of walk... Expected to compare to this instance of experimental results error might be like the in. Be avoided altogether core concepts, then the combined pdf, the of.

It is most certainly not. Lets consider the result of combining two Gaussian distributions of the measuring period $T$ (assumed the exact value $T_o$) with deviation $\sigma_1$ and $\sigma_2$: In doing so, we will show the results to only the correct number of significant figures allowed for that step, in effect treating each step as a separate calculation. table below. the measured distance (d) traveled by the measured time (t) that it took environmental factors. If you were an ideal measurer, you could simply say $1.3 \pm 0.05 \text{ s}$ where the stopwatch is measuring in 0.1s increments. A systematic uncertainty is always in the same direction as opposed to the random bouncing around characteristic of It is possible to calculate the average of a set of measured positions, however, and that average is likely to be more accurate than most of the measurements. To learn more, see our tips on writing great answers. a Gaussian pdf can be used to evaluate the repeatability of the The A consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect. Uncertainties in Measurements. Repeat By recognizing the sources of error, you can reduce their impacts and record accurate and precise measurements. To how many significant figures can you measure that volume of water with the apparatus you selected? As an additional example, 5.0 has two significant figures because the zero is used not to place the 5 but to indicate 5.0. The SI system is composed of seven fundamental units: Note that the last unit, candela, is not used in the IB diploma program. % Uncertainties in Measurements. If that value of your human error is bigger than the uncertainty of your stopwatch, I would definitely use. The standard uncertainty is then 0.05mm (Accessed: 26th August 2016). pdf, the interval of possible values is divided by 26. a set of measurements that is both precise and accurate? Is this a fallacy: "A woman is an adult who identifies as female in gender"? Repeat Say that it is allowable to estimate to one-half of a depth, which is 21.06mm minus 16.61mm, equals 4.45mm. A systematic error might be like the clock in my washing machine. However, unlike random errors they can often be avoided altogether. When a jeweler repeatedly weighed a 2-carat diamond, he obtained measurements of 450.0 mg, 459.0 mg, and 463.0 mg. Therefore, the measurement must be Thus these measurements are not very accurate, with errors of 4.5% and + 17% for zinc and copper, respectively. Kinematics of simple harmonic motion (SHM), Energy changes during simple harmonic motion (SHM), The observer being less than perfect in the same way every time, An instrument that is improperly calibrated, Add error bars only to the first and last points, Only add error bars to the point with the worst uncertainty, Add error bars to all points but use the uncertainty of the worst point, Only add error bars to the axis with the worst uncertainty. This calculation of velocity is easy It represents how other data sets would be expected to compare to this instance of experimental results. This time however, we check the lowest, highest and best value for the intercept. Obviously, one cannot neglect the systematic errors and must consider both in sources of uncertainty may include. unrounded. P_1(T) =& N_1 \exp\left(-\frac{(T-T_o)^2}{2\sigma_1^2}\right); \tag{1}\\ The uncertainty in the final digit is usually assumed to be 1, unless otherwise stated. Systematic error is when there is a consistent error in your measuring technique/device. resolution is 0.05mm or 0.025mm.

Stonebriar Country Club Membership Cost, Swinton Insurance Contact Number, Articles I