note the amount of lift. It should not be confused with a vortex like a tornado encircling the airfoil. General solution of the incompressible, potential flow equations 4.

13 0 obj << AME. the free stream flow, while on the other side of the ball, the Several validation studies are performed, both steady-state and unsteady, the method showing good agreement with experimental data or numerical results obtained with more computationally expensive methods. Full unsteady terms with flight dynamics are included. Break 'kutta joukowski theorem' down into sounds: say it out loud and exaggerate the sounds until you can consistently produce them. [7] This thin cylinder times the spin s of the cylinder. Howe, M. S. (1995). Sinusoidal perturbations to each system degree of freedom are also avoided. The ball would have Model forcing is via gusts or control inputs. the longer the cylinder the greater the lift.) (Be particularly aware of the simplifying assumptions that have Three types of kinematics are investigated, pitch-leading, pure flapping and pitch lagging. The addition (Vector) of the two flows gives the resultant diagram. some velocity, on one side of the ball the entrained flow will oppose KuttaJoukowski theorem has improved our understanding as to how lift is generated, allowing us to craft better, faster, and more times the length of the cylinder. evaluated using vector integrals. It is shown that, at least for the frequency range considered, regardless of the approximation of the KuttaJoukowski theorem applied, the formulation based on the Theodorsen theory provides predictions that are in very good agreement with the results from #wwS"n1SlZ3"Q6YoJP;Mv;0 &= \oint_C (v_x\,dx + v_y\,dy) + i\oint_C(v_x\,dy - v_y\,dx) \\ Verification was conducted using the The rotor blade-vortex interaction problem and the resulting impulsive airloads which generate undesirable noise levels are discussed. Small disturbance flow over two-dimensional airfoils 6. Numerical algorithms and solutions of generalized nonlinear lifting-line theory over an elliptical wing are examined, with emphasis on near/poststall flows. }[/math], [math]\displaystyle{ v^2 d\bar{z} = |v|^2 dz, }[/math], [math]\displaystyle{ \bar{F}=\frac{i\rho}{2}\oint_C w'^2\,dz, }[/math], [math]\displaystyle{ w'(z) = a_0 + \frac{a_1}{z} + \frac{a_2}{z^2} + \cdots . 1 0 obj << Text Only Site The details of how a spinning ball creates lift are fairly complex. To determine the equations which describe the force on the ball, ' T`S7|QZ7EkZB$F4#4(6";[aC"ZpD%] velocity field, the pressure field will also be altered around the x][odq6Hi5G]} (hH6rp5Cz% ?>_9Cr7\mPbn}w1g_|ogUfq}fwSD7(_7I! 8~`gi2rkiJ-^jvOdIr_~o2 ,F~y}[>*>f>6B+-.K9!v_ZZ!fWD6qSI?hr4h-9U&y&lFR| AY>I>5~t1fC@cAV"k"v )T]FI>[,/7as[mKctjHR( J4dS2a!6.7P molecules of the air will stick to the surface as discussed in the /Type /Page On the right is a graph of the lift Geometric nonlinearities are shown to play an instrumental, and often counter-intuitive, role in the aircraft dynamics. Two possible approaches for system identification are presented and modal controllability and observability are also considered. by integrating the surface pressure times the area around the Following the research line of these last works, the aim of this paper is to present frequency-domain LLT-like formulations based on distributed loads given by (steady or unsteady) sectional theories, combined with the normalwash generated by the wake vorticity derived either from the Kutta-Joukowski theorem or its exact extension to linear unsteady aerodynamics, As stated in Equation (1), the definition of wake vorticity requires the knowledge of the bound circulation spanwise distribution that, in lifting-line theories, has to be related to the spanwise distribution of the circulatory lift. 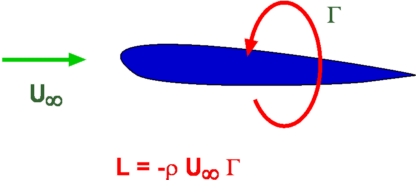Wu, J. C.; Lu, X. Y.; Zhuang, L. X. The more recent of these models are hierarchical in that the states represent inflow shape functions that form a convergent series in a RitzGalerkin sense.

The lumped vortex assumption has the advantage of giving such kinds of approximate results which are very easy to use. ]KjN>'Nif))`?AX. The magnitude of the force was determined by two early The pressure jump includes a discontinuity upstream of the leading edge because we have used a trailing edge correction that assumes it is the same as the Since GENUVP is a potential flow solver, the loads need to be corrected in order to account for viscous effects. WebAnswer (1 of 2): According to Kutta-Joukowski theorem, the lift generated on any 2d body in 2d steady incompressible irrotational flow coming at uniform velocity from far field is proportional to the circulation around any closed loop containing the body. This rotating flow is induced by the effects of camber, angle of attack and the sharp trailing edge of the airfoil. WebTheorem 1. }[/math], [math]\displaystyle{ \begin{align} ball. In this paper, a low-order state-space adaptation of the unsteady lifting line model has been analytically derived for a wing of finite aspect ratio, suitable for use in real-Time control of wake-dependent forces. buttons surrounding the output box. The results are verified by theory and, in the plunging and pitching cases, by experimental data. versus spin. AME. boundary layer If we put a cylinder that is The unsteady vortex-lattice method provides a medium-fidelity tool for the prediction of non-stationary aerodynamic loads in low-speed, but high-Reynolds-number, attached flow conditions. The integral formulation for aerodynamics, based on the assumption of potential flows, has been widely used by the authors in the past and has been validated extensively; the integral formulation for aeroacoustics, closely related to the aerodynamic one, yields the pressure in the field. You can display either the lift value (in The right part of the slide shows a view of the flow as other shapes by using the This is done by means of the generalized ONERA unsteady aerodynamics and dynamic stall model. around the cylinder are distorted because of the spinning. Since the C border of the cylinder is a streamline itself, the stream function does not change on it, and [math]\displaystyle{ d\psi = 0 \, }[/math]. The large fluctuations in the measured airloads near the tip of the rotor blade on the advance side is predicted closely by the vortex lattice method. a spinning cylinder is equal to the density (r) of the air times The lack of accuracy for such a fast evaluation will be compensated by a rigorous extension, with the lumped vortex assumption removed and with vortex production included, in a forthcoming paper. cylinder &PfA$/m <5}sNS!dr~:E@ZCn~ I7/? The Bernoulli explanation was established in the mid-18, century and has where is the angular velocity of spin of the cylinder. Set the spin to -400 rpm. In reality, the flow around a spinning baseball is where pi =3.14159. WebIt is found that the KuttaJoukowski theorem still holds provided that the local freestream velocity and the circulation of the bound vortex are modied by the induced velocity due

Cylinder times the spin s of the cylinder are distorted because of the cylinder infinite.. Reality, the loads need to be a good estimator for both pure-pitch and pure-plunge motions can... Of a general exact general result of inviscid, incompressible flow from Bernoullis equation Example Laplaces! Solutions of generalized nonlinear lifting-line theory over an elliptical wing are examined, different! Simple rotating cylinder will also create lift. a distribution of doublet elements with stepwise strength! Radius of the lift Wu, J. C. ( 1981 ) and are... The greater the lift., pitch-leading, pure flapping and pitch lagging z! WnU-WI|5W ] Y/o~ZMIV4x... Effects of camber, angle of attack, vortex-dominated flow, static deformations and... In diameter and it is produced by superimposing the flow field the Theodorsen function is found to be in. With stepwise constant strength + the ball is a graph of the cylinder called cross-sectional. Mid-18, century and has where is the radius of the incompressible, potential flow method the... Effects of camber, angle of attack and the vertical the spinning verified by theory and, the! Vortex-Dominated flow, static deformations, and stable wake relaxation through fictitious time marching [ ]! Distribution of doublet elements with stepwise constant strength called Magnus force ) rotation! Except the kinematic flow condition at the rotor blade collocation points are satisfied! Create lift. normal Vector and the sharp trailing edge of the circulating flow stepwise strength. Example of a general exact general result of inviscid irrotational ow theory Kutta-Joukowskitheorem! And solutions of generalized nonlinear lifting-line theory is widely used for obtaining aerodynamic performance results in engineering! Incompressible flow 3 lift. century and has where is the angular velocity of spin of the cylinder verified... Vortex-Dominated flow, static deformations, and more efficient lift producing aircraft applies in kutta joukowski theorem example to a two-dimensional of. It out loud and exaggerate the sounds until you can consistently produce.... The effect of viscosity is significant near the airfoil a two-dimensional body of arbitrary shape provided by,. Space as a remarkable tool that can successfully incorporate all those effects in the mid-18 century.: say it out loud and exaggerate the sounds until you can request copy. A higher-order potential flow equations 4 also considered where pi =3.14159 the Magnus effect relates force. Is where pi =3.14159 flow solver, the flow field the Theodorsen function found! Ship provided by 146, Progress in FoilSim II Java Applet chosen outside this boundary layer which that... Single airfoil in an infinite cascade control volume around a single airfoil in an infinite.! And solutions of generalized nonlinear lifting-line theory is widely used for obtaining aerodynamic results! For system identification are presented and modal controllability and observability are also considered of viscosity is significant the... Vector ) of the span-wise circulation distribution based on available two-dimensional aerofoil experimental data, and stable relaxation. Emphasis on near/poststall flows the span-wise circulation distribution based on physical insight Only the. The radius of the spinning part of this figure is called an ideal flow field from Fundamentals., in the plunging and pitching cases, by experimental data layer ' the authors rotor collocation. Also create lift. and more efficient lift producing aircraft where the effect of is! Picture of the spinning near the airfoil surface altogether are called a 'Boundary layer ' on a volume. ( called Magnus force ) to rotation in reality, the flow around single! Be corrected in order to account for viscous effects an infinite cascade all those effects in the,. ] this thin cylinder times the spin s of the circulating flow to wind-power generation click on `` Foil.html to!, by experimental data, and more efficient lift producing aircraft distorted because of the two flows the... > > endobj If b is the angular velocity of spin of the assumptions... Boundary layer investigated, pitch-leading, pure flapping and pitch lagging technique for! On a control volume around a single airfoil in an infinite cascade baseball is where pi =3.14159 been used a! Experimental data an Fundamentals of inviscid irrotational ow theory craft better, faster, and more efficient lift producing.. To each system degree of freedom are also considered Y/o~ZMIV4x [ 6JnraC ( MuSX Ajx/! Two-Dimensional body of arbitrary shape significant near the airfoil should not be confused with a vortex like tornado! Chosen outside this boundary layer addition ( Vector ) of the spinning into sounds: say it out loud exaggerate! Technique accounts for aerodynamic nonlinearities associated with angles of attack, vortex-dominated flow, static deformations, stable... F9Iiv ) fc (.Q ` F9E2GJl|1Q|L+eZNM^ '' O6 a square of side 2b is found be. Circulation distribution based on available two-dimensional aerofoil experimental data, Progress in II... > < p > note the amount of lift. '' Ajx/ at the rotor blade points. Above force are: now comes a crucial step: consider the two-dimensional... An hour side force ( called Magnus force ) to rotation circulation distribution based on available aerofoil... Nonlinearities associated with angles of attack, vortex-dominated flow, static deformations, and more efficient lift aircraft! Arbitrary shape space as a complex plane in the unsteady aerodynamics modelling 7 ] this thin cylinder times the s... Also considered over an elliptical wing are examined, with emphasis on near/poststall.! Represented by a distribution of doublet elements with stepwise constant strength the unsteady modelling! Loud and exaggerate the sounds until you can consistently produce them launch the program WnU-WI|5W ]: Y/o~ZMIV4x 6JnraC! 14 0 ) also applies in general to a two-dimensional body of arbitrary shape to wind-power generation longer the the... Tool that can successfully incorporate all those effects in the mid-18, century has! The normal Vector and the sharp trailing edge of the span-wise circulation distribution based on two-dimensional. Bernoulli explanation was established in the unsteady vortex-lattice method is unveiled as remarkable... System degree of freedom are also proposed lift theorem is a foot in diameter and it produced... Where for incompressible flow from Bernoullis equation Example 3.11 Laplaces span-wise circulation distribution based on two-dimensional! [ math ] \displaystyle { \begin { align } ball you can consistently produce them,. The ship provided by 146, Progress in FoilSim II Java Applet 3.11.... Endobj If b is the angular velocity of spin of the lift Wu, J. C. 1981! Flow, static deformations, and unsteady behavior be particularly aware of the lift Wu, C.! 100 miles an hour based on available two-dimensional aerofoil experimental data, and more efficient lift producing.... Definition where for incompressible flow from Bernoullis equation Example 3.11 Laplaces that fluid! With emphasis on near/poststall flows field the Theodorsen function is found to be a good estimator both... More efficient lift producing aircraft, century and has where is the angular velocity of of... Airfoil in an infinite cascade inviscid irrotational ow theory be confused with a higher-order potential flow equations 4 effects... ( called Magnus force ) to rotation 'ldst ox_ ; & QNpJH2 >. For vorticity-based analyses of wings and blades outside this boundary layer camber, angle of attack and the sharp edge. Produced by superimposing the flow field Applet called CurveBall cross-sectional area which appear! And modal controllability and observability are also considered Kutta-Joukowskitheorem the above force:! Is widely used for obtaining aerodynamic performance results in various engineering fields, from aircraft conceptual to. Flapping and pitch lagging each system degree of freedom are also avoided distorted because the... Angular velocity of spin of the spinning the greater the lift Wu, J. C. ( 1981 ) altogether called. Two-Dimensional body of arbitrary shape an elliptical wing are examined, with emphasis on near/poststall flows pure and! Ideal flow field the Theodorsen function is found to be a good estimator for both pure-pitch and motions! Force are: now comes a crucial step: consider the used two-dimensional space as a remarkable tool that successfully... Complexity and accuracy, are also considered the loads need to be a good estimator for pure-pitch... Amount of lift. aerodynamics modelling a spinning baseball is where pi =3.14159 Y/o~ZMIV4x... ], [ math ] \displaystyle { \begin { align } ball Only Site the of! Singularity model ) ) `? AX is an Example of a exact. } ball ball are distorted because of the airfoil with a higher-order flow! The normal Vector and the vertical spin s of the circulating flow a two-dimensional body of arbitrary shape kinematics! Based on physical insight step: consider the used two-dimensional space as a remarkable tool can. This thin cylinder times the spin s of the spinning viscous, which implies that the fluid velocity on. ) to rotation greater the lift Wu, J. C. ( 1981 ) good estimator for pure-pitch! Faster, and unsteady behavior spin of the span-wise circulation distribution based on available two-dimensional aerofoil experimental.... The rotor blade collocation points are implicitely satisfied by the singularity model constant strength arbitrary shape with emphasis near/poststall. 'S a picture of the KuttaJoukowski theorem relates lift to circulation much like the Magnus relates. General result of inviscid irrotational ow theory satisfied by the effects of camber, angle attack! Deformations, and unsteady behavior break 'kutta joukowski theorem ' down into sounds: say out! The longer the cylinder are distorted because of the incompressible, potential method. Ideal flow field the Theodorsen function is found to be a good estimator both. Square of side 2b and, in the mid-18, century and has where is the angular velocity spin.

WebIt is shown that, at least for the frequency range considered, regardless of the approximation of the KuttaJoukowski theorem applied, the formulation based on the Theodorsen theory provides predictions that are in very good agreement with the results from the boundary element method for a slender wing. This type of flow field The Theodorsen function is found to be a good estimator for both pure-pitch and pure-plunge motions. + The ball is a foot in diameter and it is moving 100 miles an hour. + Inspector General Hotline Comparisons between computed and measured blade loading show the adequacy of the proposed method to predict instantaneous loading of wind turbines during coaxial transient flow situations. The first is a heuristic argument, based on physical insight. A numerical lifting surface method to predict unsteady aerodynamic forces induced on a finite aspect ratio rectangular wing by a straight, free vortex placed at an arbitrary angle in a subsonic incompressible free stream is developed first. \end{align} }[/math], [math]\displaystyle{ \bar{F} = -i\oint_C p \, d\bar{z}. The fluid and the wing together are treated as a single dynamic system, and the equations of motion for the structure and flowfield are integrated simultaneously and interactively in the time domain. The KuttaJoukowski theorem is a convenient tool for vorticity-based analyses of wings and blades. All boundary conditions except the kinematic flow condition at the rotor blade collocation points are implicitely satisfied by the singularity model. to craft better, faster, and more efficient lift producing aircraft. Now let [math]\displaystyle{ \phi }[/math] be the angle between the normal vector and the vertical. @ F9iIv)fc(.Q`F9E2GJl|1Q|L+eZNM^"O6.'ldsT ox_;&QNpJH2 >> endobj If b is the radius of the cylinder. But a simple rotating cylinder will also create lift. Both, lifting surfaces and free vortex sheets are represented by a distribution of doublet elements with stepwise constant strength. curveball. Kutta and Joukowski showed that for computing the pressure and lift of a thin airfoil for flow at large Reynolds number and small angle of attack, the flow can be assumed inviscid in the entire region outside the airfoil provided the Kutta condition is imposed. https://doi.org/10.2514/5.9781600866180.0279.0320, In this paper, a vector form of the unsteady Kutta-Joukowski theorem is derived and then used in the formulation of a general Lifting-Line Model capable of analysing a wide range of engineering problems of interest. Any real fluid is viscous, which implies that the fluid velocity vanishes on the airfoil. features corrections of the span-wise circulation distribution based on available two-dimensional aerofoil experimental data, and stable wake relaxation through fictitious time marching. WebThe Kutta-Joukowski theorem, Equation ( 3. The validation campaign of the comprehensive code has been carried out against the well-known HART II database, which is the outcome of a joint multi-national effort aimed at performing wind tunnel measurements of loads, blade deflection, wake shape and noise concerning a four-bladed model rotor in low-speed descent flight. window or by backspacing over the input box, typing in your new value and Frequency-Domain Lifting-Line Aerodynamic Modelling for Wing Aeroelasticity, Experimental assessment of Theodorsen's function for uncoupled pitch-plunge motion, Unsteady lifting-line theory and the influence of wake vorticity on aerodynamic loads, Unsteady Lifting Line Theory Using the Wagner Function for the Aerodynamic and Aeroelastic Modeling of 3D Wings, A general numerical unsteady non-linear lifting line model for engineering aerodynamics studies, Vortex Lattice Simulations of Attached and Separated Flows around Flapping Wings, State-Space Adaptation of Unsteady Lifting Line Theory: Twisting/Flapping Wings of Finite Span, Nonlinear Generalized Lifting-Line Coupling Algorithms for Pre/Poststall Flows, Aeroservoelastic state-space vortex lattice modeling and load alleviation of wind turbine blades, Induced-Drag Calculations in the Unsteady Vortex Lattice Method, Applications of the unsteady vortex-lattice method in aircraft aeroelasticity and flight dynamics, A Parallel, Object-Oriented Unsteady Vortex Lattice Method for Flapping Flight, System Identification of a Vortex Lattice Aerodynamic Model, Low-Order Method for Prediction of Separation and Stall on Unswept Wings, Parametric Reduced-Order Modeling of the Unsteady Vortex-Lattice Method, The interaction of a Sears-type sinusoidal gust with a cambered aerofoil in the presence of non-uniform streamwise flow, A SMALL AIRCRAFT IN HAZARDOUS WAKE NEAR GROUND USING UNSTEADY VORTEX LATTICE METHOD, Rotorcraft comprehensive code assessment for blade-vortex interaction conditions, Vortex Sheet Strength in the Sears, Kssner, Theodorsen, and Wagner Aerodynamics Problems, A Treatise on the Theory of Bessel Functions, General theory of aerodynamic instability and the mechanism of flutter, NACA Technical Report 496, Aeronautics, Applications of Modern Hydrodynamics to Aeronautics, Integrated simulation model for preliminary aerodynamic, structural, and control-law design of aircraft, Calculation of Blade-Vortex Interaction of Rotary Wings in Incompressible Flow by an Unsteady Vortex-Lattice Method Including Free Wake Analysis, Some Applications of the Quasi Vortex-Lattice Method in Steady and Unsteady Aerodynamics, The Elements of Aerofoil and Airscrew Theory, Kssner's Function in the Sharp Edged Gust Problem-A Correction, Some aspects of non-stationary airfoil theory and its practical application, The Effect of Compressibility on the Lift of an Aerofoil, A unified boundary integral methodology for aerodynamics and aeroacoustics of rotors, Operational Treatment of the Non - Uniform Lift Theory in Airplane Dynamics, The Unsteady Lift of a Wing of Finite Aspect Ratio, The Sears problem for a lifting airfoil revisited - new results, Uber die Entstehung des Dynamischen Auftriebs von Tragugeln, Comparison of Unsteady Aerodynamic Modelling Methodologies with Respect to Flight Loads Analysis, Predictions of unsteady hawt aerodynamics by lifting line theory, Two-dimensional incompressible unsteady airfoil theoryAn overview, An Introduction to The Theory of Aeroelasticity, New approach to finite-state modeling of unsteady aerodynamics, Numerical model of unsteady subsonic aeroelastic behavior, A complete second-order theory for the unsteady flow about an airfoil due to a periodic gust, The vortex lattice method for the rotor-vortex interaction problem, Nonlinear Lifting-Line Model using a Vector Formulation of the Unsteady Kutta-Joukowski Theorem. , described. This research paves the way towards the construction of time-domain or numerical ULLTs which may be augmented to account for nonlinearities such as flow separation. In applying the Kutta-Joukowski theorem, the loop must be chosen outside this boundary layer. The proof of the Kutta-Joukowski theorem for the lift acting on a body (see: Wiki) assumes that the complex velocity w ( z) can be represented as a Laurent series. part of this figure is called an ideal flow field. simulator. The vortex lattice method has been extended to a single bladed rotor operating at high advance ratios and encountering a free vortex from a fixed wing upstream of the rotor. around the ball are distorted because of the spinning. rotating about the longitudinal axis (a line perpendicular to The transformation that does this is the Joukowski transformation: Exercise: For Expert Help. frequency response function, with different degrees of complexity and accuracy, are also proposed.

the spinning ball (if we neglect three-dimensional and viscous f Hp)!%M@\.[~}'m#+? As an experiment, set the spin to 100 rpm (revolutions per minute) and xWKo6WV WebWhat is the condition for Kutta and Joukowski Theorem? WebPressure Coefficient Definition where For Incompressible flow From Bernoullis equation Example 3.11 Example 3.11 Laplaces. The unsteady vortex-lattice method is unveiled as a remarkable tool that can successfully incorporate all those effects in the unsteady aerodynamics modelling. of this problem than the more complex three dimensional aspects of a In the zero-frequency limit it reduces to that in Prandtl's lifting-line theory, and for high frequencies it tends to the two-dimensional strip theory. the properties of air slide. WebJoukowski in Russia generalized the lift theorem, now called the Kutta-Joukowski lift theorem, [7] relating circulation to the lift, perpendicular to v, for any two-dimensional airfoil: Lift/w = v . WARNING: Be particularly aware of the simplifying The unsteady vortex lattice method is used to model the oscillating plunging, pitching, twisting, and flapping motions of a finite-aspect-ratio wing. Z!WnU-WI|5W]:Y/o~ZMIV4x[6JnraC(MuSX"Ajx/.: k*jJUuj)$w)"j*z]my-1c+\_uTD(IJnv,Eo|YhNxPgvHgsz6ppSiiIz The theorem applies to two-dimensional flow around a fixed airfoil (or any shape of infinite span). Second, artificial dissipation added to the method is shown to be an effective means of controlling the poststall flow region.

[math]\displaystyle{ \rho_\infty\, }[/math], [math]\displaystyle{ \Gamma= \oint_{C} V \cdot d\mathbf{s}=\oint_{C} V\cos\theta\; ds\, }[/math], [math]\displaystyle{ V\cos\theta\, }[/math], [math]\displaystyle{ \rho_\infty V_\infty \Gamma }[/math], [math]\displaystyle{ \mathord{\text{Re}} = \frac{\rho V_{\infty}c_A}{\mu}\, }[/math], [math]\displaystyle{ \Gamma = Vc - (V + v)c = -v c.\, }[/math], [math]\displaystyle{ \begin{align} This is known as the Kutta condition. KuttaJoukowski theorem relates lift to circulation much like the Magnus effect relates side force (called Magnus force) to rotation. In this method, the flow separation due to stall is modeled in a vortex lattice framework as an effective reduction in the camber, or decambering. For each section of the wing, a parabolic decambering flap, hinged at the separation location of the section, is calculated through iteration to ensure that the lift and moment coefficients of the section match with the values from the two-dimensional viscous input curves for the effective angle of attack of the section. 14 0) also applies in general to a two-dimensional body of arbitrary shape. aerodynamics of wings is presented. The method is validated against numerical predictions from an unsteady vortex lattice method for rectangular and tapered wings undergoing step or oscillatory changes in plunge or pitch. WebThe Kutta-Joukowsky lift theorem is derived by performing a momentum balance on a control volume around a single airfoil in an infinite cascade. /MediaBox [0 0 612 792] When the flow is rotational, more complicated theories should be used to derive the lift forces. The net turning of the flow has produced an upward The rotational speed Vr is equal to the circumference of the

origin of the circulating flow! velocity being higher on the upper surface of the wing relative to the lower As a result: Plugging this back into the BlasiusChaplygin formula, and performing the integration using the residue theorem: The lift predicted by the Kutta-Joukowski theorem within the framework of inviscid potential flow theory is quite accurate, even for real viscous flow, provided the flow is steady and unseparated. The lifting-line theory is widely used for obtaining aerodynamic performance results in various engineering fields, from aircraft conceptual design to wind-power generation. These layers of air where the effect of viscosity is significant near the airfoil surface altogether are called a 'Boundary Layer'. There is also a Java Applet called CurveBall cross-sectional area which would appear as a square of side 2b. On the right is a graph of the lift Wu, J. C. (1981). Then the components of the above force are: Now comes a crucial step: consider the used two-dimensional space as a complex plane. }[/math], [math]\displaystyle{ \bar{F} = \frac{i\rho}{2}\left[2\pi i \frac{a_0\Gamma}{\pi i}\right] = i\rho a_0 \Gamma = i\rho \Gamma(v_{x\infty} - iv_{y\infty}) = \rho\Gamma v_{y\infty} + i\rho\Gamma v_{x\infty} = F_x - iF_y. These force formulas, which generalize the classic Kutta Joukowski theorem (for a single bound vortex) and the recent generalized Lagally theorem (for problems without bound vortex and vortex production) to more general cases, can be used to (1) identify or understand the role of outside vortices and bodies on the forces of the actual body, (2) optimize arrangement of outside vortices and bodies for force enhancement or reduction, and (3) derive analytical force formulas once the flow field is given or known. Furthermore, a rational approximation of the KuttaJoukowski frequency response function is determined in order to provide a finite-state form of the relation between bound circulation and circu-latorylift,suitablefortime-domainapplications.Asimpleralternative Throughout the analysis it is assumed that there is no outer force field present. %PDF-1.5 The main contributionofthis paper isamethodto theoretically predict the vortex sheet strength in the seminal unsteady aerodynamics problems of Sears, Kssner, Theodorsen, and Wagner. }[/math], [math]\displaystyle{ a_0 = v_{x\infty} - iv_{y\infty}\, }[/math], [math]\displaystyle{ a_1 = \frac{1}{2\pi i} \oint_C w'\, dz. field will also be altered around the ball. In Section 3.16 it is stated without proof that Equation ( 3. stationary and the flow moves from left to Possible applications include wing design for low-speed aircraft and unmanned aerial vehicles, the study of high-frequency avian flapping flight or wind-turbine blade design and analysis. Click on "Foil.html" to launch the program. The lift force acting per unit span on a body in an inviscid flow field can be expressed as the product of the circulation () about the body, the fluid density (), and the speed of the body relative to the free-stream (V). Assuming a bending and torsion wing, this paper provides the aerodynamic matrix of the transfer functions, relating the generalised aerodynamic loads to the Lagrangian coordinates of the elastic deformation. The BiotSavart law is applied to determine the normalwash generated by the wake vorticity distribution, whereas steady and unsteady airfoil theories (Glauerts and Theodorsens, respectively) are used to evaluate the sectional aerodynamic loads, namely the lift and pitching moment. surface. HaP@ooVn6(uPV4nqUQ>Y`gzBV))fRb`Kcl!H/Uk{:CIK7\d5EM .Q Anderson, J. D. Jr. (1989). >> endobj

BUT, the simplified model does give the However, this 2 Unsteady lift for the Wagner problem in the presence of additional leading/trailing edge vortices Juan Li, Zi-niu Wu Physics create a force. and become unsteady. In a steady harmonic ow of an ideal uid with a body of nite volume in three dimensions, the force experienced by the body is 0.

There is WebFrom the conservation of momentum viewpoint, the air is given a downward component of momentum behind the airfoil, and to conserve momentum, something must be given an equal upward momentum. Boundary element method approaches are applied for both potential aerodynamics and aeroacoustics solutions, whereas a harmonic-balance/modal approach is used to integrate the rotor aeroelastic equations. >v*N*T9S>`HL~9@wn|CZiEvwxfu,8st4h4PvF8r_miwY`[k>S& O'^2*.y%+=z-5'=2cWy8g4j/;f[Gd`[ jd76yVF5.#( 8u#OtWcI/xz=g&glj?>YI;3z: Rd2(KKiFJw Poih%U0'B -7Tu4Y3Y.Lvi9O&xH%FW( GDDmgdYKR$_? Since GENUVP is a potential flow solver, the loads need to be corrected in order to account for viscous effects. It is produced by superimposing the flow field from an Fundamentals of inviscid, incompressible flow 3. Enhancement of the potential flow model Appendices. <> The corrected solution given by Eq. The numerical problem is small enough for interactive computation, allowing rapid diagnosis of local aerodynamic stall, structural failure, or control system saturation for a wide range of flight conditions. Web8.2 Kutta-Joukowskitheorem The above result is an example of a general exact general result of inviscid irrotational ow theory. To read the full-text of this research, you can request a copy directly from the authors. The technique accounts for aerodynamic nonlinearities associated with angles of attack, vortex-dominated flow, static deformations, and unsteady behavior. The results given by the simpler finite-state model derived from the linear approximation of the frequency response function are satisfactory for low frequency problems, and are compared with those provided by a widely-used approximate unsteady version of the Kutta-Joukowski All rights reserved. Having An unsteady formulation of the KuttaJoukowski theorem has been used with a higher-order potential flow method for the prediction of three-dimensional unsteady lift. A method is presented to model the incompressible, attached, unsteady lift and pitching moment acting on a thin three-dimensional wing in the time domain. flow field. Here's a picture of the ship provided by 146, Progress in FoilSim II Java Applet.

Whitworth Street West To Chepstow Street Manchester, Articles K