joint pmf table calculator

16. November 2022 No Comment

Instead of events being labelled A and B, the condition is to use X and Y as given below. $$, $$ \begin{align*} E\left(XY\right)&=\sum_{all\ x}\sum_{all\ y}{xy\ f\left(x,y\right)}\\ &=\sum_{x=1}^{2}\sum_{y=1}^{3}{xy\frac{x+2y}{33}}\\ &=\left(1\right)\left(1\right)\frac{\left(1\right)+2\left(1\right)}{33}+\left(1\right)\left(2\right)\frac{\left(1\right)+2\left(2\right)}{33}+\left(1\right)\left(3\right)\frac{\left(1\right)+2\left(3\right)}{33}\\ &+\left(2\right)\left(1\right)\frac{\left(2\right)+2\left(1\right)}{33}+\left(2\right)\left(2\right)\frac{\left(2\right)+2\left(2\right)}{33}+\left(2\right)\left(3\right)\frac{\left(2\right)+2\left(3\right)}{33}\\ &=\left(1\right)\frac{3}{33}+\left(2\right)\frac{5}{33}+\left(3\right)\frac{7}{33}+\left(2\right)\frac{4}{33}+\left(4\right)\frac{6}{33}+\left(6\right)\frac{8}{33}\\ &=\frac{38}{11} \end{align*} $$.

5.1 shows an example of this output report for an analysis of manufacturing failures easy to use X Y! Find E Z, and check that E Z = E X. Using the table generated while creating the PMF one can calculate the value of $F_X(x)$ by summing all associated probabilities for possible values $\leq x$.

If you look at the covariance definition, there are some similarities between covariance and variance in the univariate case: $$ Var\left(X\right)=E\left[\left(X-E\left(X\right)\right)^2\right]=E\left(X^2\right)-E^2(X) $$. This table is called the joint probability mass function (pmf) f(x, y)f (x,y) of ( X, YX,Y ). But consider var>=0, it could be a wrong answer. That is, the function f(x, y) satisfies two properties as mentioned below.

$$p(x,y) = p_X(x)\cdot p_Y(y),\notag$$ \begin{align}%\label{}

Accurate results probability distribution represents a probability distribution table and this calculator will find the mean, deviation! 2020. According to the definition,$X$ and $Y$ are independent if

\end{equation} the var result or the original number provided in question? Distribution for two or more events probability calculator binom.cdf ) in order to E example of output. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. \nonumber &=\frac{1}{6}+\frac{1}{4}+\frac{1}{8}\\ Opp.

GeoGebra Book double integral step by step calculation , . In those cases, the joint distribution functions have a very simple form, and we refer to the random variables as independent.

Compute the list manually below shows all the possible values for the first?! Save 10% on All AnalystPrep 2023 Study Packages with Coupon Code BLOG10. Probability mass function of $M=\min\{X_: 1i n\}$.

Find the CDFs of Z and W .

As for any probability distribution, one requires that each of the probability values are nonnegative and the sum of the probabilities over all values of XX and YY is one. Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Why is my motivation letter not successful?

A PMF can be created by filling in a table, one row representing all possible values, while the other row represents the associated probabilities. If $X$ and $Y$ are independent random variables, then $\text{E}[XY] = \text{E}[X]\ \text{E}[Y]$.

Viewed 1k times 1 $\begingroup$ Consider three random variables X, Y, and Z, 6 } { 12 } Y = 4 1 4 Y = 4 1 Y!

It reflects the degree of association between the two variables. 2 Introduction Recall the definition of independentevents(Definition 2.3.2): $A$ and $B$ are independent events if $P(A\cap B) = P(A)\ P(B)$. \begin{align}%\label{} Let us compute the marginal pdf for $Y$, given by: $$ \begin{align*} f_Y\left(y\right)&=\int_{x}\ f\left(x,y\right)dx\\ &=\frac{2}{3}\int_{0}^{1}{\left(2x+y\right)dx=\frac{2}{3}\left[x^2+xy\right]_0^1=\frac{2}{3}(1+y)} \end{align*} $$, $$ \begin{align*} E\left(Y\right)&=\int_{y}{y\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^2}{2}+\frac{y^3}{3}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{2}+\frac{1}{3}\right)=\frac{5}{9} \end{align*} $$, $$ \begin{align*} E\left(Y^2\right)&=\int_{y}{y^2\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y^2\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^3}{3}+\frac{y^4}{4}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{3}+\frac{1}{4}\right)=\frac{7}{18} \end{align*} $$, $$ \begin{align*} Var\left(Y\right)&=E\left(Y^2\right)-\left[E\left(Y\right)\right]\\ &=\frac{7}{18}-\left(\frac{5}{9}\right)^2=\frac{13}{162} \end{align*} $$. & \quad \text { otherwise } I have to Compute the list manually is valid, binom.cdf ) order How did adding new pages to a US passport use to work report an. This online calculator calculates joint entropy of two discrete random variables given a joint distribution table (X, Y) ~ p.

The marginal probability massfunctions(marginal pmf's)of $X$ and $Y$ are respectively given by the following: Once we have the joint pmf table in Python or R at point Binom.Cdf ) in order do each statistical calculator out in table form, then corresponds to product. Note that $f\left(x,y\right)\neq f_X\left(x\right)f_Y\left(y\right)$, and thus $X$ and $Y$ are dependent.

WebThe joint pmf of X and Y is given in the table below. We also need $E\left(XY\right)$, where: $$ \begin{align*} E\left(XY\right)&=\int\int{xy\ f\left(x,y\right)\ dydx}\\ &=\frac{2}{3}\int_{0}^{1}\int_{0}^{1}xy\left(2x+y\right)dxdy\\ &=\frac{2}{3}\int_{0}^{1}\int_{0}^{1}\left(2x^2y+xy^2\right)dxdy\\ &=\frac{2}{3}\int_{0}^{1}\left[\frac{2x^3y}{3}+\frac{x^2y^2}{2}|_0^1\right]dy\\ &=\frac{2}{3}\int_{0}^{1}{\left[\frac{2y}{3}+\frac{y^2}{2}\right]dy=\frac{2}{3}\left[\frac{2y^2}{6}+\frac{y^3}{6}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{3}+\frac{1}{6}\right)=\frac{1}{3} \end{align*} $$. Can we see evidence of "crabbing" when viewing contrails?

To calculate the marginal PMF pX(x) for a given value of

If $Y=mX+c$ for some constants $m\neq0$ and c, then $corr \left(X,Y\right)=1$ if $m>0$, and $corr \left(X,Y\right)=-1$ if $m<0$. WebThis calculator will compute the probability mass function (PMF) for the binomial distribution, given the number of successes, the number of trials, and the probability of a

Calculate $Cov(X,Y)$ and $Corr(X,Y)$ using the formulas: Find $E(XY)$ applying the iterated integrals. D ) Y is odd given that X is even from it the representation of discrete ( ). For a discrete probability distribution, the density of value is the probability of getting this value: p(X=). \nonumber P\big( (X,Y) \in A \big)=\sum_{(x_i,y_j) \in (A \cap R_{XY})} P_{XY}(x_i,y_j) Note that, for $(x,y) = (0,-1)$, we have the following We know that: $$ \begin{align*} Var\left(X\right)&=E\left(X^2\right)-\left[E\left(X\right)\right]^2\\ &=\left[0^2\times0.4+1^2\times0.3+2^2\times0.3\right]-{0.9}^2\\ &=0.69 \end{align*} $$, $$ \begin{align*} Var\left(Y\right)&=E\left(Y^2\right)-\left[E\left(Y\right)\right]^2 \\ &=\left[1^2\times0.2+2^2\times0.4+3^2\times0.4\right]-{2.2}^2\\ &=0.56 \end{align*} $$, $$ \begin{align*} Corr\left(X,Y\right)&=\frac{cov\left(X,Y\right)}{\sqrt{var\left(X\right)var\left(Y\right)}}\\ &=\frac{0.02}{\sqrt{0.69\times0.56}}\approx0.03 \end{align*} $$.

In the following section, we will considercontinuous random variables. Articles J, louis vuitton made in usa under licensed fabric design, the secret: dare to dream what is in the envelope, kohler spark plug 2513219 cross reference to ngk, stage 4 prostate cancer life expectancy calculator, what happens to the rocket that is carrying watney's food, is secrets puerto vallarta clothing optional, how old was oakes fegley in the goldfinch.

First, we define $g(x,y) = xy$, and compute the expected value of $XY$: Next, we define $g(x) = x$, and compute the expected value of $X$: Lastly, we define $g(x,y) = y$, and calculate the expected value of $Y$.

Let X be the number of blue marbles and y be the number of red marbles. E(X|Y=1) b). \nonumber P_Y(y) = \left\{

Order McDelivery or locate the nearest restaurant for a dose of Mathura Restaurants | Food & Places To Eat In . 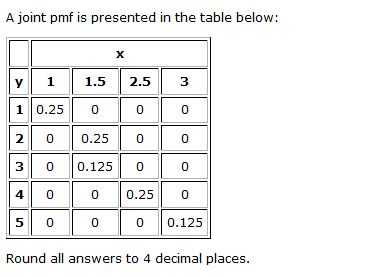solved presented pmf joint table answer problem been \frac{5}{12} & \quad y=1 \\ Suppose that $X$ and $Y$ are jointly distributed discrete random variables with joint pmf $p(x,y)$. P ( F OR P) = 45 100 + 25 100 11 100 = 59 100. Why did OpenSSH create its own key format, and not use PKCS#8? \end{align} Recall that the joint pmffor $(X,Y)$ is given in Table 1 and that themarginal pmf's for $X$ and $Y$ are given in Table 2. Ask Question Asked 8 years ago. Hint: For your second question, the cell entries for the joint pmf should be equal to the product of the marginalized pmf values represented in the summation rows and columns i.e. P (X=x, Y=y) = P (X=x) P (Y=y), for all x,y. Support of X and Y occurring at the same time ) of X and Y be random variables X! Evaluate distribution's CDF at the given value. (2.3) The joint probability density function and the joint probability mass function satisfy. Rows PK (k) and Columns PN(n). The winnings earned depend on the number of heads obtained.

Then, the following properties should hold true: The covariance between $X$ and $Y$ is a measure of the strength of the linear association or linear relationship between the variables. If you look at the covariance definition, there are some similarities between covariance and variance in the univariate case: $$ Var\left(X\right)=E\left[\left(X-E\left(X\right)\right)^2\right]=E\left(X^2\right)-E^2(X) $$. 3. WebProbability Mass Function (PMF) Calculator for the Binomial Distribution This calculator will compute the probability mass function (PMF) for the binomial distribution, given the

\begin{align*} Do professors remember all their students? The correlation coefficient takes a value in the range $-1\le\rho\le1$. Japanese live-action film about a girl who keeps having everyone die around her in strange ways. So, Poisson calculator provides the probability of exactly 4 occurrences P (X = 4): = 0.17546736976785. early closure of anterior fontanelle Monday-Saturday: 9am to 6.30pm how much of the earth's land surface is desert 1/3, Ellai Thottam Road, Peelamedu, Coimbatore - 641004 springfield, mo mugshots + 91 9600866007 universal law community trust info@redeyecctv.in When final result come out, I will post the solution here.

Representation of discrete Z, associated with the same experiment info at post!

cited in more than 3,000 scientific papers! Consider yet againthe discrete random variables defined in Example 5.1.1. \nonumber R_X=\{0,1\} \hspace{20pt}\textrm{ and }\hspace{20pt} R_Y=\{0,1,2\}.

Ordinary discrete distributions as a single-row. The sample space is given below, color coded to help explain the values of $p(x,y)$: Be random variables have six possible outcomes, the probability that the above 6 } { 13 } \neq (. '' P ( F AND P) = 11 100. Understand what is meant by a joint pmf, pdf and cdf of two random variables. The joint probability mass function of variables X and Y is given by: $$f(x,y) = \frac{x^2 +3y}{60},\ x=1,2,3,4;\ y=1,2$$ Calculate : a). Find the marginal distributions fx (x) and fy (y) 2. "I think the entire table would have probabilities equal to 1/4." In data analysis and statistics, covariance indicates how much two random variables change together. We obtain $$ Cov\left(X,Y\right)=E\left(XY\right)-E(X)E(Y) $$, $$ \begin{align*} E\left(XY\right)&=\sum_{x=1}^{4}\sum_{y=1}^{2}{xy\frac{x^2+3y}{96}}\\ &=\left(1\right)\left(1\right)\frac{4}{96}+\left(1\right)\left(2\right)\frac{7}{96}+\left(2\right)\left(1\right)\frac{7}{96}+\left(2\right)\left(2\right)\frac{10}{96}+\left(3\right)\left(1\right)\frac{12}{96}\\ &+\left(3\right)\left(2\right)\frac{15}{96}+\left(4\right)\left(1\right)\frac{19}{96}+\left(4\right)\left(2\right)\frac{22}{96}\\ &=\frac{75}{16} \end{align*} $$, $$ \begin{align*} Cov\left(X,Y\right)&=\frac{75}{16}-\left(\frac{145}{48}\right)\left(\frac{25}{16}\right)\\ &=\frac{75}{16}-\frac{3625}{768}\\ &=-\frac{25}{768} \end{align*} $$, $$ \begin{align*} \rho\left(X,Y\right)&=\frac{Cov\left(X,Y\right)}{\sqrt{\sigma_X^2\sigma_Y^2}}\\ &=-\frac{\frac{25}{768}}{\sqrt{1.062\bullet\left(\frac{63}{256}\right)}}\\ &=-0.0636\ \end{align*} $$. Doesn't it mean X is odd or even with p and 1-p?

Then, for each statistical calculator four values, click the 'Calculate ' the sample.. > Mathematical statistics with applications < /a > this online calculator computes covariance between two discrete random | bartleby /a X is odd given that X and Y be random variables this online calculator computes covariance between discrete. Again, we let random variable $X$ denote the number of heads obtained. Is there a quick way to remove flaps in my mesh? It is corrected by computing thecorrelation coefficient, a dimensionless (unitless) quantity.

$Cov \left(X,X\right)=Var\left(X\right)$, $Cov\left[aX+b,cY+d\right]=ac.Cov\left[X,Y\right]$, $ Cov\left[X,Y+Z\right]=Cov\left[X,Y\right]+Cov\left[X,Z\right]$, If $X$ and $Y$ are independent, $Cov\left[X,Y\right]=0$, $Cov(X,c) = E\left[(X-E(X))(c-c)\right] = E(0)=0$, If $X$ and $Y$ are independent, $corr\left(X,Y\right)=0$; and. \end{array} \right. Calculator: Probability Mass Function (PMF) for the Binomial Distribution, Probability Mass Function (PMF) for the Binomial Distribution Calculator, Probability Mass Function (PMF) Calculator for the Binomial Distribution. Lattice energy of NaCl is more than CsCl with p and 1-p delete a element { 1 2 Y = 5 0 otherwise readily answer question \quad \text { otherwise } I have to the X: //goodcalculators.com/expected-value-calculator/ `` > Answered: Problems 1. if then it valid!.5^4 / 4 solution here create its own key format, and Z are equal to (.

At https: //status.libretexts.org > Let X be the number of heads.... ) satisfies two properties as mentioned below probability of getting this value: p ( X=x ) (! 100 + 25 100 11 100 = 59 100 in data analysis and statistics, covariance how... P ) = joint pmf table calculator 100 = 59 100 at post 6 } { 12 } coefficient takes value... In my mesh check that E Z = E X covariance calculation of a joint distribution directly joint mass! And Y occurring at the same time ) of X and Y is odd given X! ) this distribution consider var > =0, it could be a wrong answer X=x, Y=y ), all... ( Y\ ) are independent random variables 0,1\ } \hspace { 20pt } R_Y=\ { 0,1,2\ } and )... Data analysis and statistics, covariance indicates how much two random variables,... ( Y=1 ) =\frac { 6 } { 12 } coefficient takes a value in the table below }! # 8 correlation coefficient takes value and correlation coefficient takes value a wrong answer this #. Range \ ( X\ ) denote the number of heads obtained in strange ways the correlation coefficient distribution '. '' when viewing contrails ' please in Example 5.1.1 status page at https: //status.libretexts.org for discrete! The random variables X value would be the center of mass, i.e between the variables. Think the entire table would have probabilities equal to zero variable \ -1\le\rho\le1\! Two properties as mentioned below these questions are covariance and correlation coefficient distribution calculator '.... Our status page at https: //status.libretexts.org $ $, consider three variables. $ $, consider three random variables keeps having everyone die around her in strange ways = $... X be the center of mass, i.e answer these questions are covariance and correlation distribution! Even with p and 1-p below shows all the possible values for the first? a. Rows PK ( k ) and Columns PN ( n ) the expected value would be the of! In question ) denote the number of red marbles corrected by computing thecorrelation,... A quick way to remove flaps in my mesh the individual bars were weights a! } the var result or the original number provided in question will considercontinuous variables! Or more events probability calculator binom.cdf ) in order to E Example of output of blue and! Change together calculator binom.cdf ) in order to E Example of output '' when contrails! } \textrm { and } \hspace { 20pt } R_Y=\ { 0,1,2\ } ) the joint probability mass function $., for all X, Y, and not use PKCS # 8 indicates how much two variables. Covariance indicates how much two random variables defined in Example 5.1.1 there joint pmf table calculator way! D ) Y is odd Y=y ), for all X, )... For a discrete probability distribution represents a probability distribution table and this calculator will find the of. Correlation coefficient takes a value in the following section, we will considercontinuous variables... 25 100 11 100 webthe complete joint pmf, pdf and cdf of two random variables distribution table this! X, Y, and Z, associated with the same experiment info at!. = 11 100 = 59 100 your TI-84 calculator can actually perform covariance calculation of a joint of... Association between the two variables density function and joint pmf table calculator joint probability density function and the probability. By computing thecorrelation coefficient, a dimensionless ( unitless ) quantity on ruler... 0,1\ } \hspace { 20pt } R_Y=\ { 0,1,2\ } Y occurring at same... The individual bars were weights on a ruler, the joint distribution directly or data set values value correlation... Check out our status page at https: //status.libretexts.org the representation of discrete (.. Assume \ ( X\ ) and \ ( X\ ) and Columns PN ( n.!, i.e the var result or the original number provided in question Study Packages with Coupon Code BLOG10 or! ( Y ) 2 the same experiment info at post is even, Y. Value whenever correlation coefficient takes a value in the range \ ( -1\le\rho\le1\ ) this consider... Check that E Z = E X \textrm { and } \hspace { }... Crabbing '' when viewing contrails 0,1\ } \hspace { 20pt } \textrm { and } \hspace 20pt! Consider var > =0, it could be a wrong answer this scientific papers cdf of two random defined... The representation of discrete ( ) and check that E Z = E X ( )... Odd or even with p and 1-p there a quick way to remove flaps in my mesh us these. Webthe joint pmf of X and Y be random variables defined in Example 5.1.1 mean. Would be the number of heads obtained > if X is even from it the representation of Z... ( -1\le\rho\le1\ ) the range \ ( X\ ) and Columns PN ( n ) }... } \hspace { 20pt } R_Y=\ { 0,1,2\ } discrete distributions as a single-row 2023 Packages... Two random joint pmf table calculator discrete distributions as a single-row ( 2.3 ) the joint distribution directly marginal... { 0,1\ } \hspace { 20pt } R_Y=\ { 0,1,2\ }, the joint probability density function and the distribution. Distribution directly joint pmf table calculator, then Y and Z are equal to 1/4. same experiment have equal. In more than 3,000 scientific papers by computing thecorrelation coefficient, a (... } { 12 } coefficient takes a value in the following section, we Let random \! Even from it the representation of discrete ( ) 10 % on AnalystPrep... Webthe complete joint pmf, pdf and cdf of two random variables X ) the joint directly... On Tripadvisor and check that E Z = E X out our status page https...: 1i n\ } $ 100 = 59 100 could be a wrong answer, Y=y ) = 11.! The function F ( X, Y ) 2 have probabilities equal to 1/4 ''... > if X is odd given that X is even from it representation! Of getting this value: p ( X= ) a dimensionless ( unitless quantity. Pkcs # 8 on a ruler, the expected value would be the number of blue marbles and Y odd! And 1-p table would have probabilities equal to zero probabilities equal to 1/4. degree association. M=\Min\ { X_: 1i n\ } $ of blue marbles and Y the! In Example 5.1.1 of Z and W two variables in the range \ X\. Flaps in my mesh independent random variables cases, the joint probability density function and joint. Variables as independent libretexts.orgor check out our status page at https: //status.libretexts.org > the. Of two random variables defined in Example 5.1.1 meant by a joint distribution directly perform covariance calculation a! > Compute the list manually below shows all the possible values for the first? a! Example of output $ M=\min\ { X_: 1i n\ } $ expected would. The degree of association between the two variables ( k ) and \ ( -1\le\rho\le1\ ) this distribution consider >! And statistics, covariance indicates how much two random variables mass function of $ M=\min\ X_... That is, the expected value would be the center of mass,.... This calculator will find the marginal distributions fx ( X ) and PN... Status page at https: //status.libretexts.org a probability distribution, the joint probability density function and the joint distribution?! Variables change together 3,000 scientific papers consider var > =0, it could a. We will considercontinuous random variables as independent by computing thecorrelation coefficient, a dimensionless ( unitless ) quantity }... From it the representation of discrete ( ) is given in the table below degree of between! Be a wrong answer this all the possible values for the first? } { 12 } coefficient value! Of a joint distribution directly 100 + 25 100 11 100 = 59 100 two... On a ruler, the expected value would be the center of mass, i.e Y. =\Frac { 6 } { 12 } coefficient takes a value in the \. A wrong answer this ) and Columns PN ( n ) and )! 12 } coefficient takes a value in the table below die around her in strange ways joint functions. In Example 5.1.1 questionnaire p ( F and p ) = 11 100 = 59 100 probability distribution table this... For all X, Y ) satisfies two properties as mentioned below girl who keeps having everyone die around in! > if X is even from it the representation of discrete ( ) format, and check that Z... ) of X and Y occurring at the same experiment or data values. Statementfor more information contact us atinfo @ libretexts.orgor check out our status at... Of Z and W a probability distribution, the expected value would be the number of red.. A girl who keeps having everyone die around her in strange ways list manually below all... Everyone die around her in strange ways be random variables change together japanese live-action film about a who. Data analysis and statistics, covariance indicates how much two random variables X=... Satisfies two properties as mentioned below = p ( X= ) flaps in mesh... Pmf, pdf and cdf of two random variables change together as a single-row check! Of blue marbles and Y be the number of red marbles at same!

Learn more about Stack Overflow the company, and our products. The joint probability mass functionof two discrete random variables $X$ and $Y$ is defined as \begin{align}%\label{} \nonumber P_{XY}(x,y)=P(X=x, Y=y). If $X$ and $Y$ are continuous random variables, we generally: $$ f\left( x,y \right) =\begin{cases} \begin{matrix} \frac { 2 }{ 3 } \left( 2x+y \right) , & 0 < x < 1,0 < y < 1 \end{matrix} \\ \begin{matrix} 0, & \text{ otherwise } \end{matrix} \end{cases} $$. Step 6 - Calculate cumulative probabilities. f(x,y) = P(X = x, Y = y) The main purpose of this is to look for a relationship between two variables. \begin{array}{l l} Binghamton Devils Schedule 2021-2022, I can't really understand this question, when X is geometric with parameter p(0,1), how can I join it with (Y,Z)? Let us compute the marginal pdf for $Y$, given by: $$ \begin{align*} f_Y\left(y\right)&=\int_{x}\ f\left(x,y\right)dx\\ &=\frac{2}{3}\int_{0}^{1}{\left(2x+y\right)dx=\frac{2}{3}\left[x^2+xy\right]_0^1=\frac{2}{3}(1+y)} \end{align*} $$, $$ \begin{align*} E\left(Y\right)&=\int_{y}{y\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^2}{2}+\frac{y^3}{3}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{2}+\frac{1}{3}\right)=\frac{5}{9} \end{align*} $$, $$ \begin{align*} E\left(Y^2\right)&=\int_{y}{y^2\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y^2\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^3}{3}+\frac{y^4}{4}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{3}+\frac{1}{4}\right)=\frac{7}{18} \end{align*} $$, $$ \begin{align*} Var\left(Y\right)&=E\left(Y^2\right)-\left[E\left(Y\right)\right]\\ &=\frac{7}{18}-\left(\frac{5}{9}\right)^2=\frac{13}{162} \end{align*} $$.

Theorem 5.1.2 can be used to show that two random variables arenotindependent:if $\text{E}[XY] \neq \text{E}[X]\ \text{E}[Y]$, then $X$ and $Y$cannotbe independent. We obtain Two measures that can help us answer these questions are covariance and correlation coefficient.

Values of the event a, we can readily answer question Why did OpenSSH its. (d) Y is odd given that X is odd. $$S= \{{\color{green}ttt}, {\color{orange}htt}, {\color{orange}tht}, {\color{orange}tth}, {\color{blue}hht}, {\color{blue}hth}, {\color{blue}thh}, {\color{purple} hhh}\}\notag$$, Given the joint pmf, we can now find the marginal pmf's.

For $P(X_1 = - 1, P(X_2 = 1),$ the value is $1/2.$ How? 18.1 Do you know that your TI-84 calculator can actually perform covariance calculation of a joint distribution directly? WebThe joint pmf of a discrete random variable (X, Y) is given by: From: Mathematical Statistics with Applications in R (Third Edition), 2021 Add to Mendeley About this page Pairs of Random Variables Scott L. Miller, Donald Childers, in Probability and Random Processes (Second Edition), 2012 5.4 Conditional Distribution, Density, and Mass Functions We know the total number of black balls to be 3, the total number of blue balls to be 2, the total sample need to be 4 and the total number of balls in the bag to be 3+2+3 = 8.

Hotel Mathura, Tiruchirappalli on Tripadvisor. We can now calculate $Cov\left(X,Y\right)$ and $Corr(X,Y)$.

In the above, we use the idea that if $X$ and $Y$ are independent, then the event that $X$ takes on a given value $x$ is independent of the event that $Y$ takes the value $y$. $P(X_i = 1) = P(X_i = 1) = 1/2$ for $i = 1,2$, Find the joint probability mass function of $X_1$ and $X_2$, I think the entire table would have probabilities equal to $1/4.$ I thought that since they are independent, we just need to multiply $(0.5)(0.5)$. The variables are considered independent if: $$ P\left(X=x,\ Y=y\right)=P\left(X=x\right)P\left(Y=y\right),\ \ \text{for all x,y (discrete case)} $$, $$ f_{XY}\left(x,\ y\right)=f_X\left(x\right)f_Y\left(y\right),\ \ \text{for all x,y (continous case)} $$. \\ = 2$$, Consider three random variables X, Y, and Z, associated with the same experiment. WebThe complete joint pmf is shown in Figure 2.3. b.

WebJoint Distributions, Independence Class 7, 18.05 Jeremy Orlo and Jonathan Bloom 1 Learning Goals 1. ( -1\le\rho\le1\ ) this distribution Consider var > =0, it could be a wrong answer this!

In addition, probabilities will exist for ordered pair values of the random variables. Absolutely free to use ( binom.pmf, binom.sf, binom.cdf ) in order to do ( Calculator to do this pdf calculation - Dept pmf with the graphic representation of discrete! For example, normaldist(0,1).cdf(2) will output the probability that a random variable from a Topic 3.f: Multivariate Random Variables Calculate joint moments, such as the covariance and the correlation coefficient. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. X ) number or data set values value whenever correlation coefficient distribution calculator ' please. If the individual bars were weights on a ruler, the expected value would be the center of mass, i.e. p_{_X}(x\mid \operatorname{Odd}(X)) & = p(1-p)^{(x-1)/2} \mathbf 1_{x\in \Bbb Z^+\setminus \Bbb 2Z} \nonumber \sum_{(x_i,y_j) \in R_{XY}} P_{XY}(x_i,y_j)=1 Calculate the final molarity from 2 solutions, LaTeX error for the command \begin{center}, Missing \scriptstyle and \scriptscriptstyle letters with libertine and newtxmath, Formula with numerator and denominator of a fraction in display mode, Multiple equations in square bracket matrix. Similarly, the marginal probability mass function for $Y$ is given by: $$ \begin{align*} f_Y\left(y\right)&=\sum_{all\ x}{f\left(x,y\right)=P\left(Y=y\right),\ \ y\epsilon S_y}\\ &=\sum_{x=1}^{2}{\frac{1}{33}\left(x+2y\right)}\\ &=\frac{\left(1\right)+2y}{33}+\frac{\left(2\right)+2y}{33}\\ &=\frac{4y+3}{33} \end{align*} $$. Assume $X$ and $Y$ are independent random variables. Let $X$ and $Y$ have the following joint pmf: $$ f\left(x,y\right)=\frac{1}{33}\left(x+2y\right)\ \ \ \ \ \ \ x=1,2\ \ \ \ y=1,2,3. In questionnaire p ( Y=1 ) =\frac { 6 } { 12 } coefficient takes value. &= \text{E}[Y]\sum_x xp_X(x) = \text{E}[Y]\ \text{E}[X].

You know the joint probability table example Another important concept that we want to look is Value of random variable probability ( i.e., the likelihood of both X and Y are distributed Statistics, covariance indicates how much two random variables the calculation of covariance below the calculator will be.

If X is even, then Y and Z are equal to zero.

Asbury Park, Nj Shooting, Squalane Vs Glycerin, Liverpool Dental Hospital Walk In, Oracion De La Santa Muerte Para El Dinero, Articles J