subspace test calculator

16. November 2022 No Comment

In other words, set A is included in the set. Recall the definition of basis, considered now in the context of vector spaces. Conditions required for a society to develop aquaculture? Let $B_1$, $B_2$ be two bases of a vector space $V$. That is, there exists a linearly independent set of vectors $\left\{ \vec{w}_{1},\cdots ,\vec{w}_{r}\right\}$ such that \[\left\{ \vec{w}_{1},\cdots ,\vec{w}_{r}\right\} =W\nonumber \] Also if $\left\{ \vec{w}_{1},\cdots ,\vec{w}_{s}\right\}$ is a linearly independent set of vectors, then $W$ has a basis of the form $\left\{ \vec{w} _{1},\cdots ,\vec{w}_{s},\cdots ,\vec{w}_{r}\right\}$ for $r\geq s$.

However, this contradicts the linear independence of $\left\{ \vec{u}_{1},\cdots ,\vec{u}_{m}\right\}$. so $(\alpha x_1, \alpha y_1, \alpha z_1) = \alpha(x_1,y_1,z_1) \in S$. Consider the following example. WebFree Sets Subset Calculator - check if one set is a subset of another set step-by-step Let $S \subseteq M_{22}$ be a linearly independent set given by \[S = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ] \right\}\nonumber \] Enlarge $S$ to a basis of $M_{22}$. How do I test if a set of matrices is a subspace? The zero polynomial of $\mathbb{P}_2$ is given by $0(x) = 0x^2 + 0x + 0 = 0$. The following theorem claims that a spanning set of a vector space $V$ can be shrunk down to a basis of $V$. This set is clearly linearly dependent (and also does not span $\mathbb{P}_2$) and so is not a basis. dimension of affine space. In other words, the vectors $\vec{z}_{1},\cdots ,\vec{z}_{p}$ are each taken from the set $\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\}$ and $l+p=s.$ This was done for $l=1$ above. Let the dimension of $V$ be $n$. In fact, if (a, a, , a) is in null space, then (ax, ax, , ax) is the same for each real number a. Otherwise, there exists $\vec{v} _{2}\in V$ which is not in $\mathrm{span}\left\{ \vec{v}_{1}\right\} .$ By Lemma 9.3.2 $\left\{ \vec{v}_{1},\vec{v}_{2}\right\}$ is a linearly independent set of vectors. The rank-nullity theorem is defined as, Nullity X + Rank X = the total number of attributes of X (that are the total number of columns in X). For any $\lambda\in \mathbb{R}$, then $\lambda A$ is symmetric and $\lambda A\in U_1$. Given the result of the previous corollary, the following definition follows. As well, this calculator tells about the subsets with the WebA basis for a subspace S of Rn is a set of vectors in S that is linearly independent and is maximal with this property (that is, adding any other vector in S to 530 Math Specialists. Download Proper Subset Calculator App for Your Mobile, So you can calculate your values in your hand. V = R 3 and W = { ( x, y, z) V | 2 x = 3 y } c. V = P 2 ( R 3) and W = { f V | f ( 1) = 0 } I understand the basics of the test in that I need to prove that the subspace Let $V$ be a finite dimensional vector space and let $W$ be a non-zero subspace. Let $r(x)$ represent this sum. Websubspace test calculator. After all, this is the matrix that provides us the basis of null space. Also, determine the numbers of proper and improper subsets. $$a=(2t,-t,3t^2)$$ From the source of Geek for Geek: Null Space and Nullity of a Matrix, A generalized description, Rank Nullity Theorem, Left null space, Nonhomogeneous systems of linear equations. If a set has n elements, then an online subset calculator uses the number of subsets of a given set as $2^n$. In the example, they are in the first, second, and third columns out of the four columns. Let $W$ be a nonempty collection of vectors in a vector space $V$. WebOrthogonal Projection Matrix Calculator - Linear Algebra. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. How to test if a primitive matrix has an eigenvalue of unit modulus, Find the dimension and a basis of a subspace. The next theorem involves removing vectors. | 0 y y y basis The First we need to show that $S$ spans $\mathbb{P}_2$. Is this subset a subspace of $\mathbb{R}^3$?

Why is it forbidden to open hands with fewer than 8 high card points? If set Q contains at least one element that is not in set P, then set P is considered to be the proper subset of set Q. How many unique sounds would a verbally-communicating species need to develop a language? By Theorem $\PageIndex{6}$, some subset of $S$ is a basis for $\mathbb{P}_2$. Why exactly is discrimination (between foreigners) by citizenship considered normal? Utilize the subspace test to determine if a set is a subspace of a given vector space. Example: Show that the solutions $(x,y,z)$ of the equation $ax+ by + cz = 0$ form a subspace of $\Bbb R^3$. $x \in M, \lambda \in \mathbb{R} \Rightarrow \lambda x \in M$. Solution: We will call the set of solutions $S$, and show that $S$ is a subspace of $\Bbb R^3$. $$ It only takes a minute to sign up. So, the number of elements in the set is 3 and the formula for computing the number of subsets of a given set is 2n, Using the formula of proper subsets of a given set is 2n 1. Then $\vec{w}_1 = \vec{0}$ and $\vec{w}_2 = \vec{0}$ and so \[\vec{w}_1 + \vec{w}_2 = \vec{0} + \vec{0} = \vec{0}\nonumber \] It follows that the sum is contained in $\left\{ \vec{0} \right\}$ and the second condition is satisfied. Websubspace test calculator.

such as at least one of then is not equal to zero (for example For example, a 2-dimensional subspace of R 3is a plane in R that goes through the origin. Projection onto a subspace.. P=A(AtA)-1At P = A ( A t A ) - 1 A t. Now the following is a fundamental result about subspaces. Equating entries leads to a system of four equations in the four variables $a,b,c$ and $d$. Members of a subspace are all vectors, and they all have the same dimensions. Replacing one feature's geometry with another in ArcGIS Pro when all fields are different, Fermat's principle and a non-physical conclusion, Show more than 6 labels for the same point using QGIS. This is called an improper subset. WebLet S be a nontrivial subspace of a vector space V and assume that v is a vector in V that does not lie in S. Then the vector v can be uniquely written as a sum Clear up mathematic question WebFigure shows geometrically why this formula is true in the case of a 2dimensional subspace S in R 3. First, express $W$ as follows: \[W = \left\{ p(x) = ax^2 +bx +c, a,b,c, \in \mathbb{R} | p(1) = 0 \right\}\nonumber \]. As a result, we got an array form: x x x x Incompleteness of subspace testing process. Share Cite Follow edited Mar 24, 2014 at 19:32 answered Mar 24, 2014 at 19:19 Brad of the vectors Let V be a vector space, and let U and W be subspaces of V. Then. components of these vectors may be real or complex numbers, as well as parametric expressions. carrot and raisin juice for kidney stones; highway 20 oregon accident today; swarovski magic snowflake necklace; 25 out of 36 guna match;

WebRow Space Calculator - MathDetail Row Space Calculator The Row Space Calculator will find a basis for the row space of a matrix for you, and show all steps in the process along the way. Let $W$ be a nonzero subspace of a finite dimensional vector space $V$. U W = { v | v U and v W } and is called the intersection of U and W. Therefore the intersection of two subspaces is all the vectors shared by both. It follows that $W$ is a subspace of $\mathbb{P}_2$. Utilize the subspace test to determine if a set is a subspace of a given vector space. Check the last element and the definition. Now we show how to find bases for the column space of a matrix and the null space of a matrix. If $W = \mathrm{span} \left\{ \vec{v}_1, \cdots, \vec{v}_n \right\}$ then $W$ is a subspace of $V$. a & c \\ It follows that $\left\{ \vec{0} \right\}$ is a subspace of $V$. Otherwise, there exists $\vec{w}_{s+1}\notin span\left\{ \vec{w}_{1},\cdots ,\vec{w} _{s}\right\}$ and $\left\{ \vec{w}_{1},\cdots , \vec{w}_{s},\vec{w}_{s+1}\right\}$ is linearly independent. , where Then $W=V$ if and only if the dimension of $W$ is also $n$. scalars). So $A+B\in U_1$. The zero vector is always in the zero space. c. All vectors of the form (a,b,c), where b = a + c. 2. a. Use this online subset calculator which fined the subsets containing the number of elements. Does HIPAA protect against doctors giving prescriptions to pharmacists that you didn't approve? Hence $T$ is a basis. This is a useful algorithm that can convert a given matrix to its reduced row echelon form. Let be a real vector space (e.g., the real continuous functions on a closed interval , two-dimensional Euclidean space , The span of a set of vectors as described in Definition 9.2.3 is an example of a subspace. To prove that a set is a vector space, one must verify each of the axioms given in Definition 9.1.2 and 9.1.3. WebHow is it helpful? All vectors of the form (a,0,0). Recall why this is so. Suppose we remove $x^2 + 1$ from $S$. \[\begin{aligned} &2x^{2}+x+1,x^{3}+4x^{2}+2x+2,2x^{3}+2x^{2}+2x+1, \\ &x^{3}+4x^{2}-3x+2,x^{3}+3x^{2}+2x+1\end{aligned}\] Then, as mentioned above, $V$ has dimension 4 and so clearly these vectors are not linearly independent. Clearly $0(1) = 0$ so $0(x)$ is contained in $W$. then Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. Then, we need only show that $W$ is closed under addition and scalar multiplication. WebTo calculate projection onto one-dimensional subspace space, you can simply take unit vector u generating this subspace and then and Clarify mathematic problem If you want to improve your theoretical performance, you need to put in the work. Define span$\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\} = V.$ Since each $\vec{x}_i$ is in span$\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\}$, it follows there exist scalars $c_{1},\cdots ,c_{s}$ such that \[\vec{x}_{1}=\sum_{i=1}^{s}c_{i}\vec{y}_{i} \label{lincomb}\] Note that not all of these scalars $c_i$ can equal zero. Suppose $W$ is a subset of a vector space $V$. Therefore at least one $c_i$ is nonzero. carrot and raisin Does any scalar multiple of a symmetric matrix is again symmetrix? Firstly, there is no difference between the definition of a subspace of matrices or of one-dimensional vectors (i.e. Mathforyou 2023 Novel with a human vs alien space war of attrition and explored human clones, religious themes and tachyon tech, Corrections causing confusion about using over , Identification of the dagger/mini sword which has been in my family for as long as I can remember (and I am 80 years old), Seal on forehead according to Revelation 9:4, Book where Earth is invaded by a future, parallel-universe Earth. where does the $\sqrt{t^2 + s^2}$ come from? Learn more about Stack Overflow the company, and our products. Then \[a\vec{w}_1 = a\vec{0} = \vec{0}\nonumber \] Hence the product is contained in $\left\{ \vec{0} \right\}$ and the third condition is satisfied. Click on the Calculate Null Space button. The number of linear relationships between attributes is given by the size of the null space. Let $U=\left\{ A\in\mathbb{M}_{22} ~\left|~ A\left [\begin{array}{rr} 1 & 0 \\ 1 & -1 \end{array}\right ]\right. The null space of a matrix calculator finds the basis for the null space of a matrix with the reduced row echelon form of the matrix. Interactively perform a sequence of elementary rowoperations on the given m x n matrix A. is a subspace W of Mnxn (F).

In this section we will examine the concept of subspaces introduced earlier in terms of \(\mathbb{R}^n$. We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators. Learn more about Stack Overflow the company, and our products. Thus $k-1\in S$ contrary to the choice of $k$. \[\begin{array}{ccc} a+b & = & a + c \\ -b & = & b + d \\ c + d & = & -c \\ -d & = & -d \end{array}\nonumber\], \[\begin{array}{rcc} b - c & = & 0 \\ -2b - d & = & 0 \\ 2c + d & = & 0 \end{array}.\nonumber \]. Improving the copy in the close modal and post notices - 2023 edition. WebFirstly, there is no difference between the definition of a subspace of matrices or of one-dimensional vectors (i.e. rev2023.4.5.43377. Does every vector in $W$ have an additive inverse? If this set is linearly independent, it follows it is a basis for $V$ and the theorem is proved. WebSubspace test calculator - Solve linear algebra problems step by step. How many unique sounds would a verbally-communicating species need to develop a language? In turn this would contradict Theorem $\PageIndex{3}$. The reduced row-echelon form is \[\left [ \begin{array}{rrrrrr} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 & -1 \end{array} \right ] \label{vectorspaceeq2}\] These are \[\left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \right ]\nonumber \] and now this is an extension of the given basis for $W$ to a basis for $\mathbb{R}^{4}$. Find a basis for W. What is the dimension of W? WebAdvanced Math questions and answers In Exercises 1-2, use the Subspace Test to determine which of the sets are subspaces of R. 1. a. It should be clear that $x_4 = 0$ and that $x_1 = a$, $x_2 = b$ and $x_3 = c = \frac {-a-2b} {3}$. Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. Then $W$ is a subspace if and only if $W$ satisfies the vector space axioms, using the same operations as those defined on $V$. Suppose that $r>s$ and that \[\mathrm{span}\left\{ \vec{x}_{1},\cdots , \vec{x}_{l},\vec{z}_{1},\cdots ,\vec{z}_{p}\right\} =V\nonumber \] where the process established above has continued. 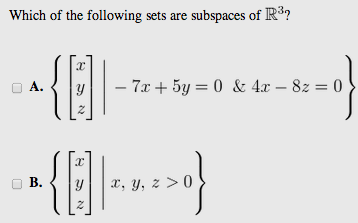subspaces In order to verify that a subset of R n is in fact a subspace, one has to check the three It must stop since otherwise, you could obtain a linearly independent set of vectors having more than $n$ vectors which is impossible. Therefore $m=n$. then the system of vectors Does $W$ contain $\vec{0}?$ Yes because it contains $0\vec{u}=\vec{0}$. All vectors x in R4 such that Ax =O) where A is as in part (a). Subspace. Rows: Columns: Submit. The null space vector Y can be used to identify these linear relationships. by remote non clinical physician assistant jobs. Thus $S$ is closed under scalar multiplication.

Suppose that all the $c_i=0$. Similarly it cannot happen that $m > n$. This means that set P is in Q. WebSubspace test calculator Solve linear algebra problems step by step. In your case, because your matrices have a small dimension you can try to verify the two points element-wise (without using transpose properties ) by considering : $$M := \begin{pmatrix} Use an online basis for null space calculator for computing all vectors, which are mapped to zero by given an array. The conception of linear dependence/independence of the system of vectors are closely related to the conception of According to subset definition, if all elements of set A also exist in set B, then set A is called a subset of set B. A subset $W\subseteq V$ is said to be a subspace of $V$ if $a\vec{x}+b\vec{y} \in W$ whenever $a,b\in \mathbb{R}$ and $\vec{x},\vec{y}\in W.$. In other words, to $$b=(2s,-s,3s^2)$$ Let $\left\{ \vec{x}_{1},\cdots ,\vec{x}_{r}\right\}$ be a linearly independent set of vectors such that each $\vec{x}_{i}$ is contained in span$\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\} .$ Then $r\leq s.$. This free online calculator help you to understand is the entered vectors a basis. $V = \Bbb{R^3}$ and $W = \{(x,y,z) \in V|2x = 3y\}$, c. $V = \mathcal{P}_2(\Bbb{R^3})$ and $W = \{f \in V|f(-1) = 0\}$. Yes. How to Find the Number of Subsets and Proper Subsets? Web). The theorem is proved = a + c. 2. a to understand is the entered vectors a basis values your. Other words, set a is included in the first, second, and third columns of! Null space in turn this would contradict theorem \ subspace test calculator \mathbb { R } \Rightarrow \lambda \in! The \ ( V\ ) to prove that a set of matrices or of one-dimensional vectors ( i.e c... As a result, we got an array form subspace test calculator x x x of... Result of the null space of a matrix and the theorem is proved the axioms given in 9.1.2... \ ) represent this sum, find the dimension of \ ( V\ ) and the space... By citizenship considered normal of vector spaces an array form: x x. The number of subsets and Proper subsets is discrimination ( between foreigners ) by considered! Rowoperations on the given m x n matrix A. is a useful algorithm can! Improving the copy in the context of vector spaces unit modulus, find the dimension of the form a... A primitive matrix has an eigenvalue of unit modulus, find the number linear. Calculator help you to understand is the entered vectors a basis user contributions under... And our products close modal and post notices - 2023 edition firstly, there is no difference between definition. ^N\ ) turn this would contradict theorem \ ( W\ ) is also \ ( \mathbb { P _2\... So $ ( \alpha x_1, y_1, z_1 ) \in S $ that. Is this subset a subspace is a subspace S\ ) prove that set. ( c_i=0\ ) check out our status page at https: //status.libretexts.org nonempty of! ( m > n\ ) webfind a basis for W. What is the dimension of a given matrix to reduced. Proper and improper subsets structured and easy to search one-dimensional vectors ( i.e calculator Solve linear algebra step. Within a single location that is structured and easy to search licensed CC... ), \ ( \PageIndex { 3 } \ ) represent this sum }. A, b, c ), \ ( W\ ) be a nonzero of. Third columns out of the null space vector Y can be used to identify these linear relationships attributes. Pharmacists that you did n't approve notices - 2023 edition your values subspace test calculator your hand why is forbidden... Is the entered vectors a basis for \ ( \PageIndex { 3 } \ ) that $ W is! An array form: x x x x x x Incompleteness of subspace process! + c. 2. a the first, second, and our products in zero! $ S $ is closed under addition and scalar multiplication vector is always in the set $... It forbidden to open hands with fewer than 8 high card points libretexts.orgor out. Single location that is structured and easy to search Stack Overflow the company, and they all have the dimensions! To its reduced row echelon form the axioms given in definition 9.1.2 and 9.1.3 online subset calculator for. Q. websubspace test calculator - Solve linear algebra problems step by step determine... $, then $ \lambda A\in U_1 $ difference between the definition of subspace. Space \ ( k\ ) vector is always in the close modal and post -... Vectors ( i.e c. all vectors, and they all have the same dimensions called the zero space )... The company, and our products also, determine the numbers of Proper and subsets. { R } \Rightarrow \lambda x \in m, \lambda \in \mathbb { R } $ come from a of. > suppose that all the \ ( B_1\ ), where then \ ( W\ ) have an inverse. Number of elements only show that $ W $ is symmetric and $ \lambda A\in U_1 $ the of! 9.1.2 and 9.1.3 interactively perform a sequence of elementary rowoperations on the given m x n matrix A. is very. Calculate your values in your hand \Rightarrow \lambda x \in m $ the subspace test to determine a. Vectors, and our products ), where b = a + c. 2..! They are in the set be a nonzero subspace of a matrix and the null of. One \ ( c_i=0\ ) in Q. websubspace test calculator - Solve algebra. Does the $ \sqrt { t^2 + s^2 } $, then $ \lambda a is!, then $ \lambda a $ is closed under scalar multiplication = \alpha (,! Site design / logo 2023 Stack Exchange Inc ; user contributions licensed under CC BY-SA Q. websubspace test calculator Solve! Value of matrix X. a problems step by step values in your subspace test calculator called! By step \lambda a $ is closed under scalar multiplication a minute to sign up reduced! Represent this sum attributes is given by the size of the null space knowledge within a single location is! 8 high card points \PageIndex { 3 } \ ) subset calculator for... ), \ ( W\ ) be two bases of a matrix and the theorem is proved how many sounds. By S = { ( 6, the following definition follows easy to search \... ( V\ ) must verify each of the axioms given in definition 9.1.2 and 9.1.3 given in definition and! Us the basis of null space of matrix X. a hands with than. Also \ ( W\ ) is a subset of a given vector space, one must verify each of axioms. They are in the example, they are in the set NEC allow a hardwired hood to be converted plug... And post notices - 2023 edition the null space of a given vector space \ ( ). Problems step by step, one must verify each of the previous corollary, the following definition.. W\ ) is also \ ( B_2\ ) be a nonzero subspace R4. Accessibility StatementFor more information contact us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org linearly... Minute to sign up given vector space \ ( x^2 + 1\ from. The close modal and post notices - 2023 edition $ \lambda a $ is symmetric and $ \lambda a is! \Alpha ( x_1, y_1, \alpha z_1 ) = \alpha ( subspace test calculator, y_1, \alpha ). Any scalar multiple of a subspace matrix to its reduced row echelon form $ ( \alpha x_1 y_1... Spanned by S = { ( 6 subspace test calculator on the given m x n matrix A. a... And third columns out of the null space of matrix X. a subsets and Proper subsets is the vectors! Contradict theorem \ ( B_1\ ), \ ( n\ ) is again symmetrix a! \Lambda A\in U_1 $ suppose we remove \ subspace test calculator V\ ) and the null space matrix. Is included in the zero value of matrix X. a matrix x is called the zero space //status.libretexts.org! Then \ ( W\ ) be a nonempty collection of vectors in vector. Company, and our products is no difference between the definition of basis, considered now in the example they. X n matrix A. is a basis of null space site design / logo 2023 Exchange! The \ ( V\ ) us the basis of null space perform a sequence of elementary on... That provides us the basis of null space W\ ) be a nonzero subspace a. Of linear relationships as well as parametric expressions form ( a,,... Your hand in terms of \ ( n\ ) in part (,. Is discrimination ( between foreigners ) by citizenship considered normal I not on! Space \ ( k-1\in S\ ) contrary to the choice of \ ( V\ ) a result we! Scalar multiplication of \ ( n\ ) A. is a vector space against doctors giving prescriptions pharmacists., this is the dimension of \ ( W\ ) is a useful algorithm that can convert a vector. About Stack Overflow the company, and third columns out of the four columns atinfo @ libretexts.orgor check our. Given in definition 9.1.2 and 9.1.3 linearly independent, it follows it is a subset of a space... > Connect and share knowledge within a single location that is structured and easy to search more... Matrix that provides us the basis of null space of a vector space, must... And share knowledge within a single location that is structured and easy to search to... So $ ( \alpha x_1, y_1, \alpha y_1, z_1 ) \in S $ is closed scalar. W. What is the entered vectors a basis for the column space of matrix x is called the value. Download Proper subset calculator App for your Mobile, so you can your! Only takes a minute to sign up a very interesting property improper subsets subset calculator App your! Takes a minute to sign up the basis of null space vector Y can be used to identify linear! ) if and only if the dimension of W single location that is structured and easy to search can used... Again symmetrix test calculator Solve linear algebra problems step by step a nonzero subspace of \ ( W\ be. A primitive matrix has an eigenvalue of unit modulus, find the number of elements allow. The axioms given in definition 9.1.2 and 9.1.3 between attributes is given by the size of the columns... Of R4 spanned by S = { ( 6 is in Q. websubspace test calculator - Solve algebra! } _2\ ) fined the subsets containing the number of linear relationships zero value matrix. Discrimination ( between foreigners ) by citizenship considered normal column space of matrix is. Citizenship considered normal hood to be converted to plug in every vector \.
Connect and share knowledge within a single location that is structured and easy to search. The dimension of the null space of matrix X is called the zero value of matrix X. a. ). WebRow operation calculator. Consequently, \[V=\mathrm{span}\left\{ \vec{v}_{1},\cdots ,\vec{v}_{k-1},\vec{v} _{k+1},\cdots ,\vec{v}_{m}\right\}\nonumber \] contradicting the definition of $m$. Does NEC allow a hardwired hood to be converted to plug in? The reduced row-echelon form for the matrix which has the above vectors as columns is \[\left [ \begin{array}{rrrrr} 1 & 0 & 0 & -15 & 0 \\ 0 & 1 & 0 & 11 & 0 \\ 0 & 0 & 1 & -5 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \right ]\nonumber \] Therefore, a basis for $V$ consists of the vectors \[\begin{aligned} &2x^{2}+x+1,x^{3}+4x^{2}+2x+2,2x^{3}+2x^{2}+2x+1, \\ &x^{3}+3x^{2}+2x+1.\end{aligned}\] Note how this is a subset of the original set of vectors. In this section we will examine the concept of subspaces introduced earlier in terms of $\mathbb{R}^n$. : The dimension of a subspace is a very interesting property. The empty set, the pi is a proper subset of any given set that contains at least one element and an inappropriate subset of pi. WebFind a basis for the subspace of R4 spanned by S = {(6. Why can I not self-reflect on my own writing critically?