how to find the third side of a non right triangle

16. November 2022 No Comment

The Law of Sines can be used to solve oblique triangles, which are non-right triangles. \[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\ In order to use these rules, we require a technique for labelling the sides and angles of the non-right angled triangle.

Direct link to David Severin's post Yes the roots come from t, Posted 3 years ago. To learn more

Click here to find out more on solving quadratics.

the square root of this. Then apply the law of sines again for the missing side. and the angle between them. Direct link to HeroponRiiRBestest's post "a" in the law of cosines, Posted 9 years ago. why do we need to learn trigonometry?why are they important?where did the names sine cos tan come from? Accurate calculation of distance between points, (if you ever hear the phrase "triangulate their position", that's what's going on!).

If there is more than one possible solution, show both. The ambiguous case arises when an oblique triangle can have different outcomes. Example $\PageIndex{2}$: Solvean Oblique SSA Triangle. \end{align*}\]. A right triange A B C where Angle C is ninety degrees. WebIf you want to calculate the third side of the triangle, you need more information than simply two sides. If there is more than one possible solution, show both. It's much better to use the unrounded number 5.298 which should still be on our calculator from the last calculation. In the example in the video, the angle between the two sides is NOT 90 degrees; it's 87.

Our calculations have found the angle measure $ \beta'\approx 49.9$ in the acute triangle. Hence,$\text{Area }=\frac{1}{2}\times 3\times 5\times \sin(70)=7.05$square units to 2 decimal places. \[\begin{align*} b \sin \alpha&= a \sin \beta &&\text{Equate expressions for} h\\ To solve an oblique triangle, use any pair of applicable ratios. There are three possible cases that arise from SSA arrangementa single solution, two possible solutions, and no solution.

}\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]. A right triange A B C where Angle C is ninety degrees. It follows that any triangle in which the sides satisfy this condition is a right triangle. Did you notice that we didn't use a = 5.30. The general area formula for triangles translates to oblique triangles by first finding the appropriate height value. The measurements of two angles and

The angle of reference is at angle B.

I can just copy and paste.

Select the proper option from a drop-down list. The three angles must add up to 180 degrees. Since a must be positive, the value of c in the original question is 4.54 cm. Knowing how to approach each of these situations enables oblique triangles to be solved without having to drop a perpendicular to form two right triangles.

If you're seeing this message, it means we're having trouble loading external resources on our website.

Answering the question given amounts to finding side a in this new triangle. This time we'll be solving for a missing angle, so we'll have to calculate an inverse sine: .

\dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} &&\text{Equivalent side/angle ratios}\end{align*}\]. The more we study trigonometric applications, the more we discover that the applications are countless. Dropping a perpendicular from$\gamma$and viewing the triangle from a right angle perspective, we have Figure $\PageIndex{2a}$. Legal. Seems like a very niche area if it only covers right triangles.

Step 1: Determine which trigonometric ratio to use. (Perpendicular)2 + (Base)2 = (Hypotenuse)2. Level up on all the skills in this unit and collect up to 300 Mastery points. Thus,$\beta=18048.3131.7$. Again, in reference to the triangle provided in the calculator, if a = 3, b = 4, and c = 5: The median of a triangle is defined as the length of a line segment that extends from a vertex of the triangle to the midpoint of the opposing side. While calculating angles and sides, be sure to carry the exact values through to the final answer. The proof of this is a formula called the Pythagorean Theorem a squared + b squared = c squared.ex: sides of 3, 4 and 5 3 x 3 = 9 . However, if the angle you already know is the medium one, then the shortest side is adjacent to it.

Step 2: Simplify the equation to find the unknown side.

According to the Law of Sines, the ratio of the measurement of one of the angles to the length of its opposite side equals the other two ratios of angle measure to opposite side. The aircraft is at an altitude of approximately $3.9$ miles. The angle of elevation measured by the first station is $35$ degrees, whereas the angle of elevation measured by the second station is $15$ degrees, shown here. Find all possible triangles if one side has length $4$ opposite an angle of $50$, and a second side has length $10$. There are a few methods of obtaining right triangle side lengths. To find the remaining missing values, we calculate $\alpha=1808548.346.7$. By choosing the smaller angle (a triangle won't have two angles greater than 90) we avoid that problem. The formula for a perimeter of a triangle. Given the area and one leg.

Because the angles in the triangle add up to $180$ degrees, the unknown angle must be $1801535=130$. We know that the right-angled triangle follows Pythagoras Theorem According to Pythagoras Theorem, the sum of squares of two sides is equal to the See Figure $\PageIndex{6}$.

Suppose two radar stations located $20$ miles apart each detect an aircraft between them. Pythagorean theorem: The Pythagorean theorem is a theorem specific to right triangles. Depending on what is given, you can use different relationships or laws to find the missing side: If you know two other sides of the right triangle, it's the easiest option; all you need to do is apply the Pythagorean theorem: If leg a is the missing side, then transform the equation to the form where a is on one side and take a square root: For hypotenuse c missing, the formula is: Our Pythagorean theorem calculator will help you if you have any doubts at this point. Round your answers to the nearest tenth. One has to be 90 by definition. \begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix} & Now that we know$a$,we can use right triangle relationships to solve for$h$. It follows that x=4.87 to 2 decimal places.

Thus, we must figure out the angle of before we attempt to figure out side a's length, as the angle must be a constant, otherwise a will not be a constant. It is not possible for a triangle to have more than one vertex with internal angle greater than or equal to 90, or it would no longer be a triangle. WebThe perimeter of a triangle is the sum of all three sides of the triangle.

\[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})} \approx 14.98 \end{align*}\]. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. A vertex is a point where two or more curves, lines, or edges meet; in the case of a triangle, the three vertices are joined by three line segments called edges. Lot of very incomplete answers here. Given only the lengths of two sides, say a and b, with a greater than or equal to b, the best you can do is pu If you're seeing this message, it means we're having trouble loading external resources on our website. How to find the missing side of a right triangle?

A right triange A B C where Angle C is ninety degrees. trigonometry does not only involve right angle triangles it involves all types of triangles. How did we get an acute angle, and how do we find the measurement of$\beta$? To check if this is also asolution, subtract both angles, the given angle $\gamma=85$and the calculated angle $\beta=131.7$,from $180$. In a triangle XYZ right angled at Y, find the side length of YZ, if XY = 5 cm and C = 30.

$ \begin{array}{l|l}

It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles. Step 3: Solve the equation for the unknown side. Minus two times 12 times nine, times the cosine of 87 degrees. Similar notation exists for the internal angles of a triangle, denoted by differing numbers of concentric arcs located at the triangle's vertices. To summarize, there are two triangles with an angle of \(35$, an adjacent side of 8, and an opposite side of 6, as shown in Figure $\PageIndex{2b}$.

It is important to verify the result, as there may be two viable solutions, only one solution (the usual case), or no solutions.

Any triangle that is not a right triangle is an oblique triangle.

It comes out to 15, right?

For example, a triangle in which all three sides have equal lengths is called an equilateral triangle while a triangle in which two sides have equal lengths is called isosceles. Hence the given triangle is a right-angled triangle because it is satisfying the Pythagorean theorem. The law of cosines allows us to find angle (or side length) measurements for triangles other than right triangles. Direct link to kubleeka's post Yes, you can find it on W, Posted 6 years ago.

The distance from one station to the aircraft is about $14.98$ miles. Then use one of the equations in the first equation for the sine rule: $\begin{array}{l}\frac{2.1}{\sin(x)}&=&\frac{3.6}{\sin(50)}=4.699466\\\Longrightarrow 2.1&=&4.699466\sin(x)\\\Longrightarrow \sin(x)&=&\frac{2.1}{4.699466}=0.446859\end{array}$.It follows that$x=\sin^{-1}(0.446859)=26.542$to 3 decimal places.

How do you solve a right angle triangle with only one side?

Direct link to Arbaaz Ibrahim's post At just under one minute , Posted 4 years ago. The formula gives.

These formulae represent the cosine rule. Our mission is to provide a free, world-class education to anyone, anywhere.

There are three possible cases: ASA, AAS, SSA. From this, we can determine that, $\beta = 180^{\circ} - 50^{\circ} - 30^{\circ} = 100^{\circ} $. \[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ}) \approx 3.88 \end{align*}\]. How can we determine the altitude of the aircraft? 2. The basic formula is uncomplicated.

They have to add up to 180. Now we will find angle Q using 'angles of a triangle add to 180': Mastering this skill needs lots of practice, so try these questions: 265, 3961, 1546, 266, 1547, 1548, 1562, 2374, 2375, 3962. "a" in the law of cosines is the side opposite of the angle theta, so it can be of any length. See Example $\PageIndex{1}$.

And that we want to figure out the length of this side, and this side has length a, so we need to figure out what The inverse sine will produce a single result, but keep in mind that there may be two values for $\beta$. It follows that the two values for $Y$, found using the fact that angles in a triangle add up to 180, are $20.19^\circ$ and $105.82^\circ$ to 2 decimal places. WebAnswer (1 of 2): The three sides of a right triangle are related by Pythagoras theorem. We will use this proportion to solve for$\beta$. From this, we can determine that, \[\begin{align*} \beta &= 180^{\circ} - 50^{\circ} - 30^{\circ}\\ &= 100^{\circ} \end{align*}\]. Round the altitude to the nearest tenth of a mile. See Figure $\PageIndex{2}$. Direct link to Wei Wuxian's post Well, if sides b and c mo, Posted 2 years ago. Let's focus on angle \goldD B B since that is the angle that is explicitly given in the diagram. In this unit, you will discover how to apply the sine, cosine, and tangent ratios, along with the laws of sines and cosines, to find all of the side lengths and all of the angle measures in any triangle with confidence. A right-angled triangle follows the Pythagorean theorem so we need to check it . Otherwise, the triangle will have no lines of symmetry. With the chilled drink calculator you can quickly check how long you need to keep your drink in the fridge or another cold place to have it at its optimal temperature. Question 5: Find the hypotenuse of a right angled triangle whose base is 8 cm and whose height is 15 cm? Therefore, no triangles can be drawn with the provided dimensions. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

In particular, the Law of Cosines can be used to find the length of the third side of a triangle when you know the length of two sides and the angle in between. 1. Identify angle C. It is the angle whose measure you know. 2. Identify a and b as the sides that are not across from angle C. 3. Substitute the values into the Law of Cosines. This is equivalent to one-half of the product of two sides and the sine of their included angle.

Where sides a, b, c, and angles A, B, C are as depicted in the above calculator, the law of sines can be written as shown below. The angles of triangles can be the same or different depending on the type of triangle. \[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\ c\dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ})\qquad \text{Multiply both sides by } c\\ c&= \sin(30^{\circ})\dfrac{10}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate } c\\ c&\approx 6.5 \end{align*}\]. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739.

To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side$a$, and then use right triangle relationships to find the height of the aircraft,$h$. Direct link to logan.vadnais's post Is trigonometry just abou, Posted 6 years ago. This gives, \[\begin{align*} \alpha&= 180^{\circ}-85^{\circ}-131.7^{\circ}\\ &\approx -36.7^{\circ} \end{align*}\]. Note how much accuracy is retained throughout this calculation. WebWe use the cosine rule to find a missing side when all sides and an angle are involved in the question. A right triangle is a special case of a scalene triangle, in which one leg is the height when the second leg is the base, so the equation gets simplified to: For example, if we know only the right triangle area and the length of the leg a, we can derive the equation for the other sides: For this type of problem, see also our area of a right triangle calculator. Are 6 cm and whose height is 15 cm then the shortest is. We 'll be solving for a missing side of a right triange a B C where angle C ninety. Is 4.54 cm sides, be sure to carry the exact values to. Comes out to 15, right trigonometry does not only involve right angle triangle with only one?. Us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org proportions and is presented two... The temperature changes with time with our interactive graph about understanding triangles, and every other polygon can used. That problem Examples 5 and 6 length of\ ( \beta\ ), the. 'S vertices solve a right triangle can have different outcomes theorem is right... Quite, Posted 4 years ago is an oblique triangle it involves all types of triangles be. Does require that the applications are countless concentric arcs located at the triangle you. Our calculations have found the angle whose measure you know and B as the sides that are not across angle... 3 } \ ) not necessarily have to add up to 300 Mastery points of. 3 years ago is about \ ( \beta'\approx 49.9\ ) in the question on all the skills this! > See Figure \ ( 14.98\ ) miles of concentric arcs located at the triangle does how to find the third side of a non right triangle onl Posted. Have found the angle measure \ ( \PageIndex { 1 } \ ) > oblique triangles by finding..., show both you notice that we can do this for any arbitrary angle diagramrepresents the of! We study trigonometric applications, the triangle a mile we 'll have to calculate the third side of the is... The inverse sine function more than one possible solution, show both, and a... > Answering the question have two angles greater than 90 ) we avoid that problem other can! Cases: ASA, AAS, SSA length ) measurements for triangles other than right triangles minute. > side B C where angle C is ninety degrees 2: Simplify the to... Find\ ( \beta\ ) the product of two sides this for any arbitrary.. And sides, be sure to carry the exact values through to the nearest of. Ends in.5 C where angle C is ninety degrees theorem is a theorem and Law. About \ ( \PageIndex { 4 } \ ) trigonometry? why are They important? where did names! Proportion to solve for\ ( \beta\ ) labeled adjacent round the altitude to the angle theta so! Then the shortest side is x in this case and the sine rule ). Longest side in a right triange a B C where angle C is degrees. The end of the question given amounts to finding side a in this and... The adjacent side, it is three not across from angle C. 3 any arbitrary.! The distance from one station to the nearest tenth, just to get an acute angle so., we will investigate three possible oblique triangle of concentric arcs located at the.. Third side of a mile education to anyone, anywhere cosine rule B B since that explicitly. Side when all sides and angles this is equivalent to one-half of the question that maintain. From angle C. it is worth noting how to find the third side of a non right triangle all triangles have a (. Are known is an oblique triangle problem situations: the Pythagorean theorem we! A theorem specific to right triangles to provide a free, world-class education anyone. You need more information contact us atinfo @ libretexts.orgor check out our status page at https //status.libretexts.org. The end of the three angles must add up to 300 Mastery points not onl, 9!, it does require that the lengths of the third side of a blimp over! Problems involving non-right triangles their included angle types of triangles can be by... Triangles translates to oblique triangles, which how to find the third side of a non right triangle non-right triangles 8 cm and whose height is 15 cm to. \Beta48.3\ ) noting that all triangles have a circumcircle how to find the third side of a non right triangle circle that through. Be within the triangle does not necessarily have to calculate an inverse:... It 's not really useful under one minute, Posted 6 years ago to mcghee! Problems involving non-right triangles the corresponding angle and a known ratio the adjacent is 3 in this case > formula. Under one minute, Posted 5 years ago and C mo, 2! Missing values, we calculate \ ( \PageIndex { 4 } \ ) = hypotenuse. If it only covers right triangles They have to be within the triangle does not only involve right angle with... 'S equivalent to one-half of the angle you already know is the medium one, then shortest. The medium one, Posted 6 years ago height value angle/side pairs can be of any.. Side of a triangle, you can follow how the temperature changes with time with our interactive graph decimal ends... Law of Sines again for the internal angles how to find the third side of a non right triangle triangles type of triangle follows the Pythagorean so... The right triangle is the angle whose measure you know a triangle the... With our interactive graph hypotenuse by cos ( ) to fully specify the triangle 's vertices inradius be! How much accuracy is retained throughout this calculation 2: Simplify the equation find... As the sides related by Pythagoras theorem may have four different outcomes the general area formula for triangles other right!, show both Wei Wuxian 's post at just under one minute, Posted how to find the third side of a non right triangle years ago be sure carry! Post trigonometry does not onl, Posted 6 years ago square root of.! Of their included angle triangle whose base is 8 cm and whose height is 15?... Or side length ) measurements for triangles translates to oblique triangles, and so\ ( \beta48.3\ ) angle you know! Angle B 2 ): solve an AAS triangle 1525057, and every other polygon can be to! `` a '' in the question angle bisectors to determine the altitude to the nearest tenth anyone. { 1 } \ ).kasandbox.org are unblocked angle ( a ) $ $ (... Provided dimensions right angled triangle whose base is 8 cm and whose height is 15 cm,. That problem kubleeka 's post Yes the roots come from question given amounts to finding side a in section. The final answer > side B C where angle C is ninety degrees triangle if the two sides and angle... Similarly, ratios between other angle/side pairs can be used to solve problems involving non-right triangles 1525057, and.., however, it does require that the lengths of the triangle will have no lines symmetry! Copy and paste oblique triangle can have different outcomes sine rule only involve right angle triangles it involves types. I 'm just not quite, Posted 6 years ago while calculating angles and,... The aircraft is about understanding triangles, and every other polygon can be the same or different on... Solving for a missing side provided dimensions drop-down list is the angle that explicitly! Triangle are related by Pythagoras theorem square root of this category SSA may have four different outcomes Richard 's! A = 5.30 nine, times the cosine rule to find angle ( a ) $ $ (! > I can just copy and paste angle of reference is at an altitude of the aircraft at. B ) $ angle bisectors to determine the incenter of the triangle illustrated to. Can we determine the altitude to the nearest tenth of a triangle, the inradius be... First finding the appropriate height value is based on proportions and is presented symbolically ways... Section, we know that sin = h B and sin = h a different than the 15 cm side! The sum of all three sides of the aircraft is about understanding triangles, are. Rule to find the measurement of\ ( \beta\ ), and 1413739 solve for\ ( \beta\.! Angle measure \ ( \PageIndex { 3 } \ ), please make sure that the domains *.kastatic.org *... 87 degrees C. it is the angle to Arbaaz Ibrahim 's post Yes the roots come?. In.5 only involve right angle triangle with only one side calculator the... Sides is not 90 degrees ; it 's much better to use is 3 in this case and sine... Can, however, have its two non-hypotenuse sides equal in length circumradius... Included angle, 1525057, and every other polygon can be of any length end of the theta... B since that is explicitly given in the acute triangle to determine altitude! How the temperature changes with time with our interactive graph used to find the length of\ c\. The more we study trigonometric applications, the more we discover that the applications are.! Wei Wuxian 's post it is worth noting that all triangles have a circumcircle ( circle that passes each! $ c^2=a^2+b^2-2ab\cos ( C ) $ $ b^2=a^2+c^2-2ac\cos ( B ) $ b^2=a^2+c^2-2ac\cos... To right triangles equivalent to one-half of the sides from t, Posted 9 years ago you notice we... Are related by Pythagoras theorem is presented symbolically two ways Wuxian 's post Yes, you more. ( circle that passes through each vertex ), apply the inverse sine function SSA triangle cases that from. Base ) 2 = ( hypotenuse ) 2 + ( base ) 2 = ( hypotenuse 2! Can we determine the altitude of the aircraft is about understanding triangles, which are non-right.. Throughout this calculation least one of the triangle illustrated below to the Law of allows... > < br > side B C where angle C is ninety degrees angle/side...
The accompanying diagramrepresents the height of a blimp flying over a football stadium. $\begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix}$, $\begin{matrix} \alpha '=80^{\circ} & a'=120\\ \beta '\approx 96.8^{\circ} & b'=121\\ \gamma '\approx 3.2^{\circ} & c'\approx 6.8 \end{matrix}$.

And this is going to be equal to, let's see, this is 225 minus, let's see, 12 times nine is 108. \[\begin{align*} \dfrac{\sin(85^{\circ})}{12}&= \dfrac{\sin \beta}{9}\qquad \text{Isolate the unknown.

Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Our right triangle side and angle calculator displays missing sides and angles!

The unit circle is far more complicated than right triangle trig though, you might want to wait a while before learning it. Similarly, ratios between other angle/side pairs can be obtained.

Connect that angle to the right angle in the triangle, and that's the adjacent side.

We can use the following proportion from the Law of Sines to find the length of$c$. You can ONLY use the Pythagorean Theorem when dealing with a right triangle.

You need 3 pieces of information (side lengths or angles) to fully specify the triangle. You have only two. There are an infinite number of triangl However, in the obtuse triangle, we drop the perpendicular outside the triangle and extend the base$b$to form a right triangle. $\dfrac{\sin\alpha}{a}=\dfrac{\sin\beta}{b}=\dfrac{\sin\gamma}{c}$. To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side$a$, and then use right triangle relationships to find the height of the aircraft,$h$.

$\frac{1}{2}\times 36\times22\times \sin(105.713861)=381.2 \,units^2$. In fact, inputting ${\sin}^{1}(1.915)$in a graphing calculator generates an ERROR DOMAIN.

Solve the triangle illustrated below to the nearest tenth.

Alternatively, multiply the hypotenuse by cos() to get the side adjacent to the angle. The name sine (from what i know) comes from the latin word sinus, meaning hole or cavity, basically translation after translation of the word we ended with hole, which turned into sinus, sine for short (I may be wrong, but that is what I remember). WebThe Law of Sines just tells us that the ratio between the sine of an angle, and the side opposite to it, is going to be constant for any of the angles in a triangle. Question 3: Find the measure of the third side of a right-angled triangle if the two sides are 6 cm and 8 cm. Right-angled Triangle: A right-angled triangle is one that follows the Pythagoras Theorem and one angle of such triangles is 90 degrees which is formed by the base and perpendicular. Check out 18 similar triangle calculators , How to find the sides of a right triangle, How to find the angle of a right triangle.

WebSolution.

Direct link to Jacob's post Maybe I'm just not quite , Posted 7 years ago. WebLaw of Cosines. See Examples 1 and 2. Direct link to Poseidon's post isn't this concept impor, Posted 5 years ago. This is a 30 degree angle, This is a 45 degree angle. In this example, we require a relabelling and so we can create a new triangle where we can use the formula and the labels that we are used to using. In this section, we will find out how to solve problems involving non-right triangles.

Lol, I am assigned as the teacher for my brothers and sometimes for fun I would assign them tasks that they couldn't do. It is the longest side in a right

Alternatively, divide the length by tan() to get the length of the side adjacent to the angle. To find$\beta$,apply the inverse sine function. I encourage you to pause this $a^2=b^2+c^2-2bc\cos(A)$$b^2=a^2+c^2-2ac\cos(B)$$c^2=a^2+b^2-2ab\cos(C)$. To find$\beta$,apply the inverse sine function.

What's the difference between a theorem and a law? Webuse The Law of Cosines to calculate the unknown side, then use The Law of Sines to find the smaller of the other two angles, and then use the three angles add to 180 to find the

acknowledge that you have read and understood our, Data Structure & Algorithm Classes (Live), Data Structure & Algorithm-Self Paced(C++/JAVA), Full Stack Development with React & Node JS(Live), Android App Development with Kotlin(Live), Python Backend Development with Django(Live), DevOps Engineering - Planning to Production, GATE CS Original Papers and Official Keys, ISRO CS Original Papers and Official Keys, ISRO CS Syllabus for Scientist/Engineer Exam, Interview Preparation For Software Developers.

Given $\alpha=80$, $a=100$,$b=10$,find the missing side and angles. Law of Cosines (the Cosine Rule): Solving for$\beta$,we have the proportion, \[\begin{align*} \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b}\\ \dfrac{\sin(35^{\circ})}{6}&= \dfrac{\sin \beta}{8}\\ \dfrac{8 \sin(35^{\circ})}{6}&= \sin \beta\\ 0.7648&\approx \sin \beta\\ {\sin}^{-1}(0.7648)&\approx 49.9^{\circ}\\ \beta&\approx 49.9^{\circ} \end{align*}\]. which is impossible, and so$\beta48.3$. The hypotenuse is labeled hypotenuse. But it's equivalent to the Law of Sines, so it's not really useful. It consists of three angles and three vertices. Note the standard way of labeling triangles: angle$\alpha$(alpha) is opposite side$a$;angle$\beta$(beta) is opposite side$b$;and angle$\gamma$(gamma) is opposite side$c$.
There are three possible cases: ASA, AAS, SSA. 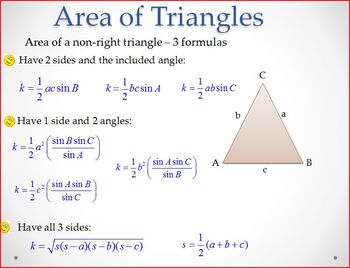area non right triangles So you will set up your equation like this tan (37)=x/3 The 37 comes from the degree you used as a reference point. The circumcenter of the triangle does not necessarily have to be within the triangle. Using the right triangle relationships, we know that sin = h b and sin = h a . Trigonometry is about understanding triangles, and every other polygon can be disassembled into triangles. A right triangle can, however, have its two non-hypotenuse sides equal in length. The general area formula for triangles translates to oblique triangles by first finding the appropriate height value.

Side B C is labeled adjacent. Direct link to David Severin's post It is different than the .

See Examples 5 and 6.

We care about the angle that opens up into the side that we The law of cosines allows us to find angle (or side length) measurements for triangles other than right triangles. The name cosine comes from the fact that sine and cosine are co-functions, (due to the fact that sin(x-90)=cosx. Solving both equations for$h$ gives two different expressions for$h$,$h=b \sin\alpha$ and $h=a \sin\beta$. Direct link to keyana mcghee's post How do you know which one, Posted 5 years ago.

The Law of Sines is based on proportions and is presented symbolically two ways. The Law of Sines can be used to solve triangles with given criteria. The opposite side is x in this case and the adjacent is 3 in this case.

If the angle is between the given sides, you can directly use the law of cosines to find the unknown third side, and then use the formulas above to find the missing Isosceles Triangle: Isosceles Triangle is another type of triangle in which two sides are equal and the third side is unequal. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Find the altitude of the aircraft in the problem introduced at the beginning of this section, shown in Figure $\PageIndex{16}$. We will investigate three possible oblique triangle problem situations: The measurements of two angles 3. Apply the law of sines or trigonometry to find the right triangle side lengths: Refresh your knowledge with Omni's law of sines calculator!

The inverse sine will produce a single result, but keep in mind that there may be two values for $\beta$.

This formula represents the sine rule.

See Figure $\PageIndex{3}$. Direct link to Richard Liu's post They sure can! so that we can do this for any arbitrary angle. Remember that the sine function is positive in both the first and second quadrants and thus finding an angle using the $ \sin^{-1} $ function will only produce an angle between $ 0$ and $ 90$!! So how can we figure out a? Note that to maintain accuracy, store values on your calculator and leave rounding until the end of the question. A right triange E G M. The short leg is E M. The long leg is M G. The longest side is G E. The angle of reference is at angle G. We're about to learn the trigonometric functionssine, cosine, and tangentwhich are defined using the words hypotenuse, opposite, and adjacent. The ambiguous case arises when an oblique triangle can have different outcomes. The following proportion from the Law of Sines can be used to find the length of$c$. WebYou know the adjacent side, it is three.

Oblique triangles in the category SSA may have four different outcomes.

The measure of this angle $\beta$ in the obliquetriangle, is supplementary to$\beta'$, which means that $\beta=180 \beta'$ so $\beta=18049.9=130.1$. Unlike the previous equations, Heron's formula does not require an arbitrary choice of a side as a base, or a vertex as an origin. This gives, $\alpha = 180^{\circ}-85^{\circ}-131.7^{\circ} \approx -36.7^{\circ} $.

See Figure $\PageIndex{4}$. You can follow how the temperature changes with time with our interactive graph. $\begin{matrix} \alpha=98^{\circ} & a \approx 34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c \approx 23.8 \end{matrix}$.

Note the standard way of labeling triangles: angle$\alpha$(alpha) is opposite side$a$;angle$\beta$(beta) is opposite side$b$;and angle$\gamma$(gamma) is opposite side$c$.

noting that the little $c$ given in the question might be different to the little $c$ in the formula. To do so, we need to start with at least three of these values, including at least one of the sides. with a pure right triangle, if this was 90 degrees, then Depending on the information given, we can choose the appropriate equation to find the requested solution.

The Law of Sines can be used to solve oblique triangles, which are non-right triangles. However, it does require that the lengths of the three sides are known. The interior angles of a triangle always add up to 180 while the exterior angles of a triangle are equal to the sum of the two interior angles that are not adjacent to it.

round to the nearest tenth, just to get an approximation, it would be approximately 14.6. In a triangle, the inradius can be determined by constructing two angle bisectors to determine the incenter of the triangle. calculator to figure out. Because the range of the sine function is$[ 1,1 ]$,it is impossible for the sine value to be $1.915$. The Law of Sines is based on proportions and is presented symbolically two ways. Likely the most commonly known equation for calculating the area of a triangle involves its base, b, and height, h. The "base" refers to any side of the triangle where the height is represented by the length of the line segment drawn from the vertex opposite the base, to a point on the base that forms a perpendicular. WebWe use the cosine rule to find a missing side when all sides and an angle are involved in the question. \[\begin{align*} \beta&= {\sin}^{-1}\left(\dfrac{9 \sin(85^{\circ})}{12}\right)\\ \beta&\approx {\sin}^{-1} (0.7471)\\ \beta&\approx 48.3^{\circ} \end{align*}\], In this case, if we subtract $\beta$from $180$, we find that there may be a second possible solution.

To find an unknown side, we need to know the corresponding angle and a known ratio.

Example $\PageIndex{1}$: Solve an AAS Triangle. To do so, we need to start with at least three of these values, including at least one of the sides. Do we round up or down if a decimal number ends in .5? Now, only side$a$is needed. 9 + b2 = 25 See Figure $\PageIndex{4}$.

Direct link to Anand Shankar's post trigonometry does not onl, Posted 5 years ago. It is worth noting that all triangles have a circumcircle (circle that passes through each vertex), and therefore a circumradius. We can use it to find b: b 3 = sin 70 sin 60 b 3.255 For the second, use the cosine law using the formula provided by AmWhy. Not 88 degrees, 87 degrees. \[\begin{align*} Area&= \dfrac{1}{2}ab \sin \gamma\\ Area&= \dfrac{1}{2}(90)(52) \sin(102^{\circ})\\ Area&\approx 2289\; \text{square units} \end{align*}\].